3473

Diffusion spectrums of intra- and extra-cellular molecular diffusion via Oscillating Gradient Spin-Echo MRI-techniques

Manuel Avellaneda^1,2, Ignacio Lembo Ferrari^1,2, and Gonzalo A. Alvarez^1,2,3
¹Instituto Balseiro, CNEA, Universidad Nacional de Cuyo, S. C. de Bariloche, Argentina, ²Centro Atómico Bariloche, CONICET, CNEA, S. C. de Bariloche, Argentina, ³Instituto de Nanociencia y Nanotecnologia, CNEA, CONICET, S. C. de Bariloche, Argentina

Synopsis

Keywords: Microstructure, Diffusion/other diffusion imaging techniques

Motivation: We address the challenge of characterizing complex diffusion spectra within biological tissues, with implications for early disease detection.

Goal(s): We aimed to employ OGSE sequences to probe water diffusion in phantom models, separating intra- and extracellular diffusion components.

Approach: Using OGSE sequences, we varied diffusion times and gradient values, effectively disentangling diffusion spectral densities and analyzing restricted diffusion patterns.

Results: We successfully separated intra- and extra-cellular diffusion spectral densities. The intra-cellular one provides the cell-sizes. In contrast, the extra-cellular spectral densities exhibited complexity, necessitating the development of models for interpretation. These insights hold promise for early disease diagnosis based on tissue-microstructure characterization.

Impact: Our study successfully separates intra- and extracellular diffusion spectral densities, enabling cell-size determination, advancing medical imaging. It fosters nuanced tissue microstructure characterization, opening new avenues for early disease diagnosis and innovative clinical applications.

Introduction

Magnetic Resonance Imaging (MRI) stands as a cornerstone in medical diagnosis, known for its non-invasive nature that ensures patient safety. Clinical MRI-scanners provide spatial resolutions at the millimeter scale, and preclinical-scanners can further refine this to tens of micrometers. Recent research suggests that by harnessing magnetic field gradient modulation sequences, one can unveil information on an even finer scale through molecular diffusion-induced decoherence^1-11. This capability holds immense promise for the early detection of conditions like neurodegenerative diseases and specific cancer-types^12-18. The Oscillating Gradient Spin Echo (OGSE) sequence^19-22, is a tool that offers this quantitative lens based on characterizing molecular diffusion within biological tissues.

In this study, we employ OGSE sequences to probe the water diffusion spectrum on phantoms as a proxy to characterize the intricate properties of both intra- and extra-cellular spaces. By delving into the diffusion time-evolution patterns and their spectral densities, our research shows how to probe selectively the intra- and extra-cellular diffusion components, and shows evidence of the complex nature of the extra-cellular diffusion. The insights gleaned from our results have the potential to bring tools for disease diagnosis based on quantitative tissue-microstructure characterizations.

Methods and theoretical foundations

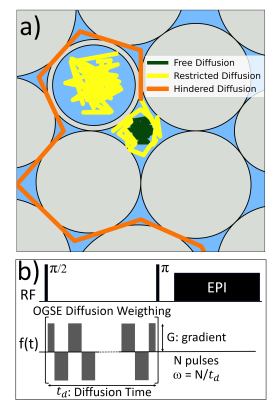
Extra-cellular space phantoms and intra/extra-cellular space phantom using yeast cells
Compacted bundles of solid aramid fibers of a diameter $$$\approx 10 \mu m$$$, submerged in water were used to represent extra-axonal spaces in white matter^23-24. The water in the phantom diffuses within the interstitial space (Fig. 1a). Then we used fresh commercial yeasts diluted in water after waiting until they were deposited at the bottom of the container. Here water diffuses within the inter- and extra-cellular spaces (Fig. 1a).

Diffusion-displacement spectral density probed by Oscillating Gradient Spin-Echo
We use OGSE sequences (Fig. 1b) in a 9.4T preclinical scanner to probe the displacement power spectrum²², represented by the spectral density $$$S(\omega)$$$. $$$S(\omega)$$$ is the Fourier transform of the autocorrelation function of the molecular position random-motion. It quantifies the translational dynamics of molecules in a given medium as a function of its fluctuation frequency modes $$$\omega$$$. The OGSE sequences involve a series of modulated gradient pulses. By adjusting the total diffusion time and the number of oscillations, we measured $$$S(\omega)$$$ across a range of frequencies.

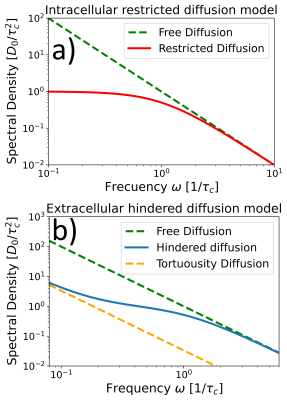
Two models were considered for $$$S(\omega)$$$ (Fig. 2): one for completely closed compartments (intra-cellular diffusion)^1-2
$$ S(\omega) = \frac{D_0 \tau_c^2}{1+\tau_c^2 \omega^2} \hspace{3cm}(1)$$
and another for hindered diffusion where compartments are interconnected (extra-cellular diffusion)^19,25 $$S(\omega) =\frac{D_0}{\alpha \omega^2}+\left(1-\frac{1}{\alpha}\right) \frac{D_0 \tau_c^2}{1+\tau_c^2 \omega^2}. \hspace{3cm}(2)$$
Here $$$D_0$$$ is the diffusion coefficient of free water, $$$\tau_c$$$ is the characteristic time required to fully explore a compartment size $$${l_c}^2=D_0 \tau_c$$$ and $$$1/\alpha$$$ is the macroscopic tortuosity coefficient.

Results and discussion

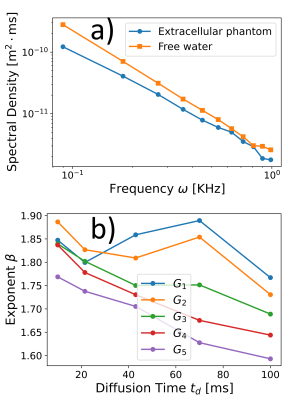
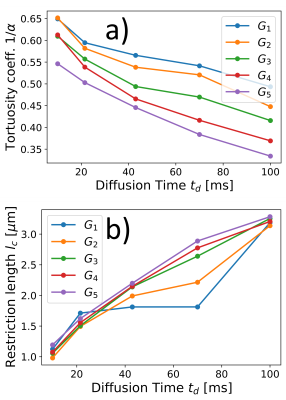
Diffusion spectral density determined from the extra-cellular phantom
Our study on the extracellular phantoms revealed a distinctive power-law behavior in the spectral density (Fig. 3). This behavior depends on the OGSE sequence parameters and does not align with the phenomenological theoretical representation for hindered diffusion of Eq. (2). Yet, we fit the experimental data using the representation of Eq. (2) to obtain apparent diffusion parameters, we found that the estimated restriction length increases and the tortuosity coefficient decreases with increasing the diffusion time $$$t_d$$$ (Fig. 4). These findings are consistent with previous observations of microscopic tortuosity mechanisms using the NOGSE sequence, highlighting the complexity of extracellular diffusion²⁴.

Yeast Cells paradigm for the spectral densities of intra/extracellular diffusion
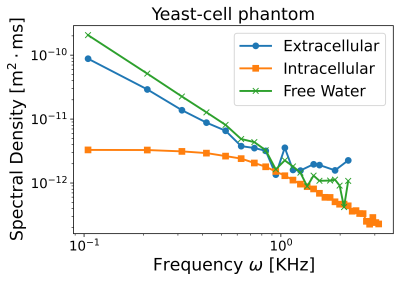
In yeast cells, we effectively separated the intra- and extracellular spectral densities (Fig. 5) by adjusting the diffusion time and gradient strength. The extracellular diffusion displayed a behavior similar to the one observed for the extracellular phantom, while intracellular diffusion agreed well with the representation of Eq. (1). From the fitted $$$\tau_c$$$, we accurately determined the expected cell diameter⁴ $$$d=(7.6 \pm 0.6) \mu m$$$. This example illustrates how gradient manipulation allowed emphasizing specific diffusion components, revealing distinct spectral densities.

Conclusions

Characterizing complex diffusion spectra, particularly when multiple regimes coexist, is a challenging task. We observed that existing models do not accurately describe the extracellular spectral density, but consistently found evidence of restricted diffusion, with compartment sizes increasing with increasing the diffusion time. In cases like yeast, where both intra- and extracellular diffusion occur, we successfully separated the spectral densities by adjusting diffusion times and gradient values. This allowed us to gain valuable insights into characteristic compartment sizes associated with restricted diffusion associated with cell-sizes. Our findings emphasize the intricacies of diffusion spectrum characterization, particularly in scenarios involving diverse diffusion regimes. These insights have the potential to enhance diagnostic tools based on tissue microstructure characterization in hope of finding early disease detection.

Acknowledgements

This work was supported by CNEA; CONICET; ANPCyT-FONCyT PICT-2017-3156, PICT-2017-3699, PICT-2018-4333, PICT-2021-GRF-TI-00134, PICT-2021-I-A-00070; PIP-CONICET (11220170100486CO); UNCUYO SIIP Tipo I 2019-C028, 2022-C002, 2022-C030; Instituto Balseiro; Collaboration programs between the MINCyT (Argentina) and, MAECI (Italy) and MOST (Israel); and Erasmus+ Higher Education program from the European Commission between the CIMEC (University of Trento) and the Instituto Balseiro (Universidad Nacional de Cuyo).

References

1. Álvarez GA, Shemesh N, Frydman L. Coherent dynamical recoupling of diffusion-driven decoherence in magnetic resonance. Phys. Rev. Lett. 2013; 111:080404.

2. Shemesh N, Álvarez GA, Frydman L. Measuring small compartment dimensions by probing diffusion dynamics via Non-uniform Oscillating-Gradient Spin-Echo (NOGSE) NMR. J. Magn. Reson. 2013; 237:49.

3. Xu J, Li H, Harkins KD, Jiang X, Xie J, Kang H, Does MD, Gore JC. Mapping mean axon diameter and axonal volume fraction by MRI using temporal diffusion spectroscopy. Neuroimage 2014; 103:10.

4. Shemesh N, Álvarez GA, Frydman L. Size distribution imaging by Non-Uniform Oscillating-Gradient Spin Echo (NOGSE) MRI. PLoS ONE 2015; 10:e0133201.

5. Alexander DC, Dyrby TB, Nilsson M, Zhang H. Imaging brain microstructure with diffusion mri: Practicality and applications. NMR Biomed. 2019; 32:e3841.

6. Novikov DS, Fieremans E, Jespersen SN and Kiselev VG. Quantifying brain microstructure with diffusion MRI: Theory and parameter estimation. NMR in Biomedicine. 2019;32:e3998.

7. Veraart J, Nunes D, Rudrapatna U, Fieremans E, Jones DK, Novikov DS, Shemesh N. Noninvasive quantification of axon radii using diffusion MRI. eLife 2020; 9:e49855.

8. Yon M, de Almeida Martins JP, Bao Q, Budde MD, Frydman L, Topgaard D. Diffusion tensor distribution imaging of an in vivo mouse brain at ultrahigh magnetic field by spatiotemporal encoding. NMR Biomed. 2020; 33:e4355.

9. Zwick A, Suter D, Kurizki G, Álvarez GA. Precision limits of tissue microstructure characterization by Magnetic Resonance Imaging. Phys. Rev. Applied. 2020; 14:024088.

10. Capiglioni M, Zwick A, Jiménez P, Álvarez GA. Noninvasive Quantitative Imaging of Selective Microstructure Sizes via Magnetic Resonance. Phys. Rev. Applied 2021; 15:014045.

11. Zwick A, Álvarez GA. Quantum sensing tools to characterize physical, chemical, and biological processes with magnetic resonance. Journal of Magnetic Resonance Open. 2023; 16-17:100113.

12. Padhani AR, et al. Diffusion-weighted magnetic resonance imaging as a cancer biomarker: Consensus and recommendations. Neoplasia 2009; 11:102.

13. Drago V., et al. Disease tracking markers for alzheimer’s Disease at the prodromal (MCI) stage. J. Alzheimers Dis. 2011; 26:159.

14. White NS, et al. Probing tissue microstructure with restriction spectrum imaging: Histological and theoretical validation. Hum. Brain Mapp. 2013; 34:327.

15. White NS, et al. Diffusion-weighted imaging in cancer: Physical foundations and applications of restriction spectrum imaging. Cancer Res. 2014; 74:4638.

16. Nilsson M, Englund E, Szczepankiewicz F, van Westen D, Sundgren PC. Imaging brain tumor microstructure. Neuroimage. 2018; 182:232-250.

17. Huang SY, Fan Q, Machado N, et al. Corpus callosum axon diameter relates to cognitive impairment in multiple sclerosis. Ann. Clin. Transl. Neurol. 2019; 6(5):882-892.

18. Xu J, Jiang X, Li H, Arlinghaus LR, McKinley ET, Devan SP, Hardy BM, Xie J, Kang H, Chakravarthy AB, Gore JC. Magnetic resonance imaging of mean cell size in human breast tumors. Magn. Reson. Med. 2020; 83:2002.

19. Stepišnik J. Time-dependent self-diffusion by NMR spin-echo. Physica B 1993; 183: 343–350.

20. Callaghan PT, Stepisnik J. Frequency-domain analysis of spin motion using modulated-gradient NMR. J. Magn. Reson. A 1995; 117:118-122.

21. Gore JC, Xu J, Colvin DC, Yankeelov TE, Parsons EC, Does MD. Characterization of tissue structure at varying length scales using temporal diffusion spectroscopy. NMR Biomed. 2010; 23:745.

22. Stepisnik J, et al. Spectral characterization of diffusion in porous media by the modulated gradient spin echo with CPMG sequence. Journal of Magnetic Resonance. 2006; 182:195.

23. Giménez M, Jiménez P, Pedraza L, Betancourth D, Zwick A, Álvarez GA. Microstructure size- distribution estimations with smooth and sharp non-uniform oscillating gradient spin-echo modulations. Proc. Intl. Soc. Mag. Reson. Med. 2021; 29:3418.

24. Saidman EL, Zwick A, Tambalo S, Feiweier T, Jovicich J, and Álvarez GA. Selective filters of translational molecular diffusion dynamics in white matter microstructures with preclinical and clinical MRI. Proc. Intl. Soc. Mag. Reson. Med. 2023; 31:0970.

25. Stepišnik J, Mohorič A., Duh A. Diffusion and flow in a porous structure by the gradient spin echo spectral analysis. Physica B 2001; 307:158–168.

Figures

Fig. 1: (a) Scheme for the considered models of intra- and extra-cellular diffusion. Different diffusion regimes are shown with spin-particle Brownian motion trajectories. (b) OGSE pulse sequence scheme used for probing the diffusion displacement power spectrum. After an excitation pulse, the OGSE modulation weights diffusion on the signal amplitude and then, after an inversion pulse to refocus inhomogeneities, encode the signal with an EPI acquisition.

Fig. 2: Diffusion displacement spectral densities $$$S(\omega)$$$. (a) Restricted diffusion representation of Eq. (1) as a model for intra-cellular diffusion, compared with the free diffusion spectrum, (b) Extra-cellular hindered diffusion representation of Eq. (2) for the displacement spectral density. It is compared with the diffusion spectrum of free diffusion, and the macroscopic tortuosity diffusion.

Fig. 3: Spectral density for water diffusion within the extra-cellular phantom. (a) The diffusion displacement spectral density observed on the phantom is compared with the one of free water diffusion, evidencing a power law behavior. (b) The power law exponent determined from fittings is shown as a function of the used diffusion time $$$t_d$$$. Different gradient strengths were used, where $$$G_i=\frac{g_i}{(t_d)^{3/2}}$$$ with $$$g_i=$$$8.45, 13.5, 21.2, 23.9 and 35.0 ms$$$^{3/2}$$$T/m, respectively to keep the b-value constant for different diffusion times.

Fig. 4: Fitting parameters of the phenomenological hindered diffusion representation of Eq. (2). They depend on the OGSE setup parameter as the diffusion time and gradient strength. The gradient strengths are the one described in Fig. 3. The tortuosity coefficient $$$1/\alpha$$$ decreases with the diffusion time $$$t_d$$$, while the restriction length $$$l_c=\sqrt{D_0 \tau_c}$$$ increases.

Fig. 5: Diffusion displacement spectral densities $$$S(\omega)$$$ for the water diffusion in the yeast cells phantom. Depending on the gradient strength used, the intra- and extra-cellular signal is measured allowing to determine selectively the corresponding spectral densities. They are compared with the one determined from free water. The extra-cellular spectrum behaves as the one observed for the extra-cellular phantom. The intra-cellular spectrum agrees well with Eq. (1), and gives an average cell-size of $$$d=(7.6 \pm 0.6) \mu m$$$.

Proc. Intl. Soc. Mag. Reson. Med. 32 (2024)

3473

DOI: https://doi.org/10.58530/2024/3473