4485
Optimization method for estimating tissue microstructure size-distributions with diffusion weighted imaging
Pablo Javier Jimenez1,2, Analia Zwick1,2,3, and Gonzalo Alvarez1,2,3
1Centro Atómico Bariloche, CONICET, CNEA, Bariloche, Argentina, San Carlos de Bariloche, Argentina, 2Instituto Balseiro, CNEA, Universidad Nacional de Cuyo, Bariloche, Argentina, San Carlos de Bariloche, Argentina, 3Instituto de Nanociencia y Nanotecnologia,CNEA, CONICET, Bariloche, Argentina, San Carlos de Bariloche, Argentina
1Centro Atómico Bariloche, CONICET, CNEA, Bariloche, Argentina, San Carlos de Bariloche, Argentina, 2Instituto Balseiro, CNEA, Universidad Nacional de Cuyo, Bariloche, Argentina, San Carlos de Bariloche, Argentina, 3Instituto de Nanociencia y Nanotecnologia,CNEA, CONICET, Bariloche, Argentina, San Carlos de Bariloche, Argentina
Synopsis
Keywords: Diffusion/other diffusion imaging techniques, Microstructure
Characterization of microstructures in living-tissues by non-invasive imaging is one of the key and outstanding challenges for diagnosing early stages of pathologies and understanding disease mechanisms. Here we implement an optimal control strategy for obtaining microstructure details by Diffusion-Weighted Imaging sequences. We estimate microstructure parameters of size-distribution models for axon bundles, attaining the ultimate precision limits predicted by quantum-information tools. We performed proof-of-principle experiments of the optimization protocol with an ex-vivo mouse-brain contrasted with simulations. These results might drastically reduce the total acquisition time compared to the present state-of-the-art, opening alternative avenues towards unraveling diagnostic information by quantitative MRI.Introduction
Characterization of microstructures in living tissues is one of the keys to diagnosing early stage of pathologies and understanding disease mechanisms. However, the non-invasive extraction of reliable information on biomarkers based on microstructure details is still a challenge1-5. Magnetic Resonance Imaging (MRI) plays an important role to address this challenge, allowing the acquisition of deep-tissue's images1-5. However, due to the weakness of nuclear spin signals, the size of features that can be resolved with noninvasive MRI is orders of magnitude larger than the relevant structures. Diffusion-weighting imaging techniques6 are a promising approach to allow quantitative estimation of morphological features of tissue microstructure that excels in the spatial resolution of conventional MRI3,7-16.We recently derived from quantum information theory the ultimate precision limits for obtaining microstructure details by DWI12-13. We here implement an optimal control strategy for obtaining such details to estimate microstructure parameters of size-distribution models for axon bundles7-11,15-17. We performed proof-of-principle simulations mimicking white matter tracts and experiments with an ex-vivo mouse brain of the optimization protocol. By attaining the ultimate precision limit per measurement, the number of measurements and the total acquisition time may be drastically reduced compared to the present state-of-the-art. These proof-of-principle results are expected to open alternative avenues toward unraveling diagnostic information by quantitative MRI.
Methods
Theoretical tools. We use information theory tools (Bayesian and Fisher Information) to determine the optimal control parameters of DWI sequences for estimating microstructure size-distributions12,13. We define an information gain function that is maximized by the sequence parameters. We consider non-uniform oscillating gradient spin-echo sequences (NOGSE) (Fig. 1) and the derived analytical expression that predicts the signal decay8-14.Information metric. As typically, quantitative parameters are extracted from experimental data from least squares fittings, we define an information gain based on the distance from the ideal target curve to a perturbed signal behavior. The maximum gain provides the optimal control parameters to extract the size-distribution.
DWI Acquisition. To verify the optimal sequence design approach, we performed proof-of-principle experiments with an ex-vivo mouse brain. MRI NOGSE images were acquired with microimaging probes in a Bruker Avance III HD 9.4T WB. We analyzed the Corpus Callosum (CC) region, which contains aligned axons whose size distribution is modeled by a LogNormal distribution9,11. We performed measurements with different gradient strengths. These measurements were taken with a diffusion time T=21.5 [ms], gradients G=12,46,50,80 [G/cm], and N=2 in Fig. 1a.
Results
We show that MRI pulse sequences can be optimized to attain the ultimate precision limits by choosing control parameters such as experimental time T and gradient strength G, that are uniquely determined by the expected size, the diffusion coefficient, and the spin relaxation time T2. We calculate the information gain function with different control parameters and get the optimal parameters in Fig. 2. These optimal parameters maximize the size-distribution information.We verified the predicted results with a series of experiments with a microimaging Bruker equipment, in the CC of the ex-vivo mouse brain. Each experiment was made with different gradients. We measured the tissue size-distributions in a specific ROI in each experiment and compared the results. For each distribution we derive the optimal gradient strength shown in the legend. Using a global analysis, based on the information from all measurements, we obtain the size-distribution shown with dashed-line. The predicted optimal gradient is consistent with the predictions from each individual experiment (see Fig.3).
Discussion
From information theory, the predicted optimal control parameter depends on the ground-truth size-distribution. Therefore, by implementing a series of experiments with different control parameters, we demonstrated the consistency of the reconstructed size-distributions and the predicted optimal control parameters. The optimal results are also consistent with global fittings, where all experimental data is used to estimate the size-distribution. Our results demonstrate that if we have an initial size-distribution guess that is close to the true size-distribution, we can obtain control parameters that are very close to the optimal and attain high precision. The optimal experimental results are consistent with predictions based on quantum information theory that predicts that the optimized parameters attain the ultimate precision limits to estimate the size-distribution12,13.Conclusion
We developed an optimization protocol for designing DWI sequences that maximize information gain to determine diffusion restriction-size distributions. We achieved the ultimate precision limits of microstructure-sizes predicted by quantum information tools. We performed proof-of-principle experiments with an ex-vivo mouse brain that showed consistency with our predictions and optimization protocol. These results might drastically reduce the total acquisition time compared to the present state-of-the-art and are expected to open alternative avenues toward unraveling diagnostic information by quantitative MRI.Acknowledgements
We acknowledge S. Esposito, V. Piatti, and M. Kortsarz for preparing the ex-vivo mouse brain. We thank J. Jovicich for fruitful discussions. This work was supported by CNEA; CONICET; ANPCyT-FONCyT PICT-2017-3156, PICT-2017-3699, PICT-2018-4333; PIP-CONICET (11220170100486CO); UNCUYO SIIP Tipo I 2019-C028, 2022-C002, 2022-C030; Instituto Balseiro; A collaboration program from MINCyT (Argentina) and MAECI (Italy) and Erasmus+ Higher Education program from the European Commission between the CIMEC (University of Trento) and the Instituto Balseiro (Universidad Nacional de Cuyo). P.J. acknowledge support from the Instituto Balseiro and CONICET fellowships. A.Z. and G.A.A. are members of the Research Career of CONICET.References
- Padhani AR, et al.,Diffusion-weighted magnetic resonance imaging as a cancer biomarker: Consensus and recommendations, Neoplasia 11, 102 (2009).
- Drago V., et al. Disease tracking markers for alzheimer’s Disease at the prodromal (MCI) stage. J. Alzheimers Dis. 26, 159 (2011).
- Callaghan P. Translational Dynamics Magnetic Resonance, Principles of Pulsed Gradient Spin Echo NMR (Oxford University Press, Oxford, 2011).
- White NS, et al. Probing tissue microstructure with restriction spectrum imaging: Histological and theoretical validation. Hum. Brain Mapp. 34, 327 (2013).
- White NS, et al. Diffusion-weighted imaging in cancer: Physical foundations and applications of restriction spectrum imaging, Cancer Res. 74, 4638 (2014).
- Alexander DC, Dyrby TB, Nilsson M, Zhang H. Imaging brain microstructure with diffusion mri: Practicality and applications. NMR Biomed. 32, e3841 (2019).
- N. Shemesh, G. A. Álvarez and L. Frydman, Measuring small compartment dimensions by probing diffusion dynamics via Non-uniform Oscillating-Gradient Spin-Echo (NOGSE) NMR, J. Magn. Reson. 237, 49 (2013).
- N. Shemesh, G. A. Alvarez, and L. Frydman, Size distribution imaging by non-uniform oscillating-gradient spin echo (NOGSE) MRI, PLoS ONE 10, e0133201 (2015).
- G. A. Álvarez, N. Shemesh and L. Frydman, Coherent Dynamical Recoupling of Diffusion-Driven Decoherence in Magnetic Resonance, Phys. Rev. Lett. 111, 080404 (2013).
- M. Capiglioni, A. Zwick, P. Jiménez, and G. A. Álvarez, Noninvasive Quantitative Imaging of Selective Microstructure Sizes via Magnetic Resonance, Phys. Rev. App. 15(1), 014045 (2021).
- A. Zwick, G. A. Álvarez and G. Kurizki. Maximizing information on the environment by dynamically controlled qubit probes. Phys. Rev. Applied 5, 014007 (2016).
- A. Zwick, D. Suter, G. Kurizki and G. A. Álvarez. Precision Limits of Tissue Microstructure Characterization by Magnetic Resonance Imaging. Phys. Rev. Applied 14, 024088 (2020).
- Giménez M, Jiménez P, Pedraza L, Betancourth D, Zwick A, Álvarez GA. Microstructure size-distribution estimations with smooth and sharp non-uniform oscillating gradient spin-echo modulations. Proc. Intl. Soc. Mag. Reson. Med. 29:3418 (2021).
- Y. Assaf, T. Blumenfeld-Katzir, Y. Yovel, and P. J. Basser, Axcaliber: A method for measuring axon diameter distribution from diffusion MRI, Magn. Reson. Med. 59, 1347 (2008).
- D. C. Alexander, P. L. Hubbard, M. G. Hall, E. A. Moore, M. Ptito, G. J. Parker, and T. B. Dyrby, Orientationally invariant indices of axon diameter and density from diffusion MRI, Neuroimage 52, 1374 (2010).
- J. Xu, H. Li, K. D. Harkins, X. Jiang, J. Xie, H. Kang, M. D. Does, and J. C. Gore, Mapping mean axon diameter and axonal volume fraction by MRI using temporal diffusion spectroscopy, Neuroimage 103, 10 (2014).
Figures
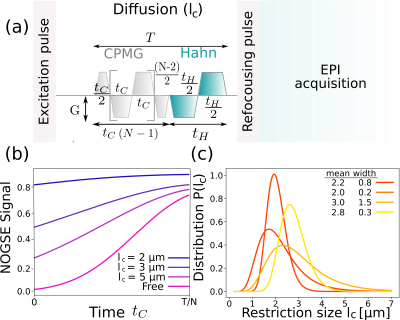
Figure 1: Schematic representation of the DWI technique for restriction size distribution estimation. (a) NOGSE sequence8,10. The control parameters are the gradient strength G, the number of refocusing periods N, the diffusion time T and the delay tC and tH. (b) Predicted NOGSE signals as a function of tC for the restriction-size size distribution shown in (c). (c) Typical restriction-size distributions of white matter tracts considered for the simulations.
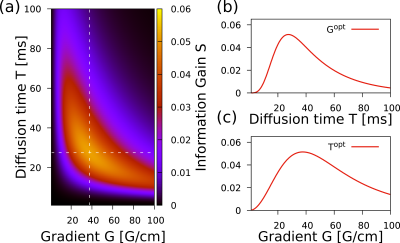
Figure 2: Information gain S based on the NOGSE signal for a given size distribution as a function of the different control sequence parameters. (a) Information gain as a function of the Gradient and the Diffusion time. This gain is maximized by the control parameters marked with white dashed-lines. (b) Gain across the vertical dashed line in (a). (c) Gain across the horizontal dashed line in (a).
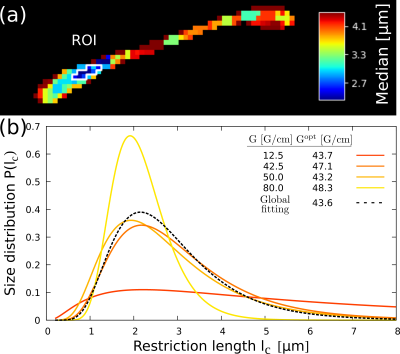
Figure 3: Proof-of-principle experiments with an ex-vivo mouse brain corpus callosum (CC). (a) CC image of the median of a log-normal distribution of restriction sizes fitted for each voxel using the analytical expression derived in Ref9. (b) Determined restriction-size distributions for the different gradient strengths used for the experiments. These distributions correspond to the marked ROI on (a). Similar results are obtained for other ROIs.
DOI: https://doi.org/10.58530/2023/4485