4052
Optimizing k-space averaging patterns for advanced denoising-reconstruction methods1Signal and Image Processing Institute, Ming Hsieh Department of Electrical and Computer Engineering, University of Southern California, Los Angeles, CA, United States
Synopsis
This work investigates the potential value of combining non-uniform k-space averaging with advanced nonlinear image denoising-reconstruction methods in the context of low-SNR MRI. A new data-driven strategy for optimizing the k-space averaging pattern is proposed, and is then applied to total variation and U-net reconstruction methods. It is observed that non-uniform k-space averaging (with substantially more averaging at the center of k-space) is preferred for both reconstruction approaches, although the distribution of averages varies substantially depending on the noise level and the reconstruction method. We expect that these results will be informative for a wide range of low-SNR MRI applications.
INTRODUCTION
Most of the current advanced MR image reconstruction methods are designed to reconstruct images from undersampled k-space data in scenarios where the signal-to-noise ratio (SNR) is relatively high. However, there is also growing interest in applying advanced MR image reconstruction methods to k-space data that is fully-sampled but contaminated by large amounts of noise, meaning that the reconstruction approach should involve some degree of denoising. Noisy k-space data is a pervasive issue that can be problematic in almost every high-resolution MRI application at every field strength, although may be especially important to address in the context of emerging high-performance low-field MRI systems.6-10In high-SNR scenarios with k-space undersampling, there has been substantial interest in the data-driven design of optimal k-space undersampling patterns.1-5 Specifically, undersampling patterns have been optimized by using a database of previous scans to determine which subset of k-space samples is likely to provide the best image reconstruction results. However, to the best of our knowledge, the issue of optimal k-space sampling is largely unexplored for low-SNR scenarios, with most of the modern denoising-reconstruction approaches assuming simply that k-space is fully sampled. In previous work involving advanced denoising-reconstruction methods, it has been generally assumed that each point in k-space is acquired with the same number of repeated measurements (i.e., “uniform averaging”).
It has been known for a long time that non-uniform averaging (with a larger number of averages near the center of k-space and fewer averages at high-frequencies) can outperform uniform averaging for simple methods like apodized Fourier reconstruction.11 More recently, the benefits of non-uniform averaging have also been suggested for quadratically-regularized reconstruction.12 As a result, there are good reasons to hypothesize that non-uniform averaging may also be beneficial for more advanced denoising-reconstruction methods. In this work, we investigate this hypothesis by proposing a new data-driven strategy for optimizing the k-space averaging pattern, and then evaluating denoising-reconstruction performance in the context of two advanced image reconstruction methods: total variation (TV) reconstruction13 and a neural network reconstruction method based on the U-net.14
METHODS
Design of Optimal Averaging PatternsWe consider a scenario in which there are $$$L$$$ possible k-space sampling locations $$$\mathbf{k}_{\ell}$$$, $$$\ell=1,\ldots, L$$$, and we wish to determine the optimal number $$$m_\ell$$$ of repeated measurements (averages) to be obtained at each location, subject to a constraint on the total number of k-space measurements.
For optimization, we assume that we have access to a database of high-SNR datasets from an application of interest, and that we can add simulated noise to mimic the effects of a low-SNR acquisition. We also assume that we are given a denoising-reconstruction procedure (which may depend on the averaging pattern). We then define an optimality criterion as the average error between each high-SNR image and the denoised image obtained by applying a given denoising-reconstruction method to simulated noisy k-space data obtained with a given averaging pattern.
In general, finding an averaging pattern that minimizes this optimality criterion is a difficult integer programming problem with combinatorial complexity. As a result, we consider a continuous relaxation of the optimization problem in which the values $$$m_\ell$$$ now represent the fractional averaging effort applied to the $$$\ell$$$th position in k-space. This is a standard relaxation approach.15
We optimize this relaxed optimality criterion using backpropagation.16 To maximize performance, we can also optimize reconstruction parameters (e.g., the neural network weights for the U-net) simultaneously as we optimizing the averaging weights. Once continuous $$$m_\ell$$$ values are obtained, they are rounded back to integers.17
Experiments
We used 2400 T2-weighted brain slices from the fastMRI dataset14 for training. The averaging pattern was initialized with uniform averaging, and the L2-norm was used to measure image reconstruction errors.
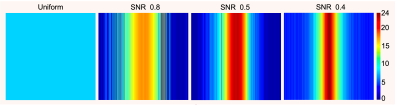
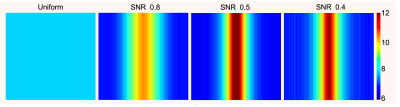
Optimized averaging was performed for three different noise levels (SNR=0.8, 0.5, and 0.4) as illustrated in Fig. 1, and reconstruction results obtained with optimized averaging patterns were compared against images obtained with conventional uniform averaging. Performance was then assessed using datasets that were not used for training.
RESULTS
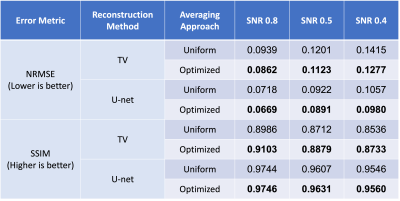
The optimized k-space averaging patterns we obtained for TV and U-Net reconstruction are shown in Figs. 2 and 3, respectively. As can be seen, the optimized averaging patterns tend to sample the center of k-space more densely, although with substantial variations depending on the image reconstruction method and the SNR level. Quantitative error metrics are reported in Table 1. The results show that in every case we tried, optimized averaging resulted in improved NRMSE and SSIM error metrics compared to uniform averaging.CONCLUSIONS
We proposed a new method for optimizing the k-space averaging pattern for advanced denoising-reconstruction methods, and tested it for TV and U-Net reconstruction applied to noisy T2-weighted brain data. Our results confirm the hypothesis that non-uniform averaging can be beneficial in this context, although the optimal averaging strategy will depend on the noise level and the characteristics of the denoising-reconstruction method. We anticipate that these results will be insightful to a wide range of low-SNR MRI scenarios.Acknowledgements
This work was supported in part by NIH grants R01-MH116173 and R01-NS074980, the Ming Hsieh Institute for Research on Engineering- Medicine for Cancer, and a USC Annenberg Graduate Fellowship.References
[1] Y. Cao, D. Levin. Feature-recognizing MRI. Magn Reson Med 30:305-317, 1993.
[2] M. Seeger, H. Nickisch, R. Pohmann, B. Scholkopf. Optimization of k-space trajectories for compressed sensing by Bayesian experimental design. Magn Reson Med 63:116-126, 2010.
[3] B. Gozcu, R. Mahabadi, Y.-H. Li, E. Ilicak, T. Cukur, J. Scarlett, V. Cevher. Learning-based compressive MRI. IEEE Trans Med Imaging 37:1394-1406, 2018.
[4] J. Haldar, D. Kim. OEDIPUS: An experiment design framework for sparsity-constrained MRI. IEEE Trans Med Imaging 38:1545-1558, 2019.
[5] C. Bahadir, A. Wang, A. Dalca, M. Sabuncu. Deep-learning-based optimization of the under-sampling pattern in MRI. IEEE Trans Comput Imaging 6:1139-1152, 2020.
[6] M. Sarracanie et al. Low-cost high-performance MRI. Sci Rep 5:15177, 2015.
[7] A. Campbell-Washburn et al. Opportunities in interventional and diagnostic imaging by using high-performance low-field-strength MRI. Radiology 293:384-393, 2019.
[8] J. Marques, F. Simonis, A. Webb. Low-field MRI: An MR physics perspective. J Magn Reson Imaging 49:1528-1542, 2019.
[9] L. Wald et al. Low-cost and portable MRI. J. Magn Reson Imaging 52:686-696, 2019.
[10] J. Marques et al. ESMRMB annual meeting roundtable discussion: “when less is more: the view of MRI vendors on low-field MRI.” MAGMA 34;479-482, 2021.
[11] T. Mareci, H. Brooker. Essential considerations for spectral localization using indirect gradient encoding of spatial information. J Magn Reson 92:229-246, 1991.
[12] J. Haldar, Z.-P. Liang. On MR experiment design with quadratic regularization. Proc IEEE ISBI 2011, p. 1676-1679.
[13] M. Lustig, D. Donoho, J. Pauly. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn Reson Med 58:1182-1195, 2007.
[14] J. Zbontar et al. fastMRI: An open dataset and benchmarks for accelerated MRI. arXiv preprint arXiv:1811.08839.
[15] F. Pukelsheim. Optimal Design of Experiments. John Wiley & Sons, 1993.
[16] D Rumelhart and G Hinton and R Williams. Learning representations by back-propagating errors. Nature 323:533-536, 1986.
[17] F Pukelsheim and S Rieder. Efficient rounding of approximate designs. Biometrika 79:763-770, 1992.
Figures
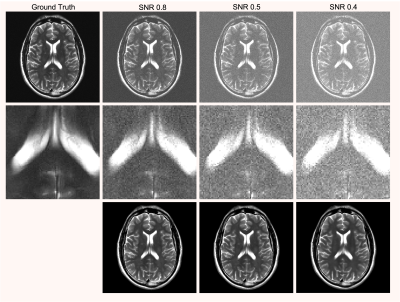
Fig. 1. The top row shows representative ground truth and noisy Fourier reconstructions with uniform averaging for different SNR values. The second row shows zoom-ins to the images from the first row to better depict image details. The bottom row shows U-net reconstructions of this data.