3598
Free-breathing, motion-resolved myocardial T1 mapping using inversion-recovery radial FLASH and model-based reconstruction1University Medical Center Göttingen, Göttingen, Germany, 2Partner Site Göttingen, German Centre for Cardiovascular Research (DZHK), Göttingen, Germany, 3Cluster of Excellence "Multiscale Bioimaging: from Molecular Machines to Networks of Excitable Cells" (MBExC), University of Göttingen, Göttingen, Germany, 4Campus Institute Data Science (CIDAS), University of Göttingen, Göttingen, Germany
Synopsis
In this work, we develop a motion-resolved model-based reconstruction for free-breathing multi-phase myocardial T1 mapping using a free-running inversion-recovery radial FLASH sequence. Initial results on an experimental phantom and two healthy subjects have demonstrated that the proposed method could achieve motion-resolved T1 mapping at a spatial resolution of 1.33 × 1.33 × 6 mm3 with good accuracy, precision and reproducibility.
Introduction
Quantitative cardiac T1 mapping is of increasing interest in clinical cardiovascular magnetic resonance (CMR) imaging [1,2]. Recent developments on free-breathing T1 mapping [3,4] have enabled high-resolution T1 mapping at multiple cardiac phases without breathhold, overcoming the limitations of the conventional breathhold techniques such as MOLLI [5] and SASHA [6]. These methods usually extract motion (respiration and/or cardiac) signals from a non-Cartesian sampled k-space center using self-gating, followed by a motion-resolved image reconstruction and pixel-wise fitting. Meanwhile, model-based reconstructions have been developed for cardiac T1 mapping [7-9]. The latter directly estimates myocardial parameter maps from k-space enabling very high acceleration. In this work, we combine these strategies using a motion-resolved model-based reconstruction for free-breathing T1 mapping with a free-running inversion-recovery radial FLASH sequence. Validations of the proposed method have been performed on an experimental phantom and two healthy subjects.Theory and Methods
Sequence Design and Motion EstimationThe free-breathing T1 mapping sequence is shown in Fig 1. It consists of 1) a non-selective inversion 2) continuous radial FLASH readout with a tiny golden-angle ~$$$23.63^\circ$$$ 3) and a time gap (5 second) between inversions to ensure recovery of the longitudinal magnetization. The above process was repeated 20 times, resulting a total acquisition time of around 3 minutes. After data acquisition, an adapted SSA-FARY technique [10] was applied on the k‐space center of all radial spokes and all coils to extract the signal component that is most relevant for respiratory motion. Cardiac motion synchronization was accomplished with the signal recorded using an external ECG device.
Motion-Resolved Model-Based Reconstruction
The acquired k-space data is sorted into 6 respiration and 17 cardiac phases. To estimate parameter maps from all phases, a previously developed model-based reconstruction [8,9] is extended: the estimation of parameter maps and coil sensitivity maps from all states is formulated as a nonlinear inverse problem:
$$\begin{equation}\begin{split}\hat{x} &= \text{argmin}_{x} \|\sum_{i=1}^{N_{{R}}}\sum_{j=1}^{N_{{C}}}F_{i,j}(x) -\widetilde{Y}_{i,j} \|_{2}^{2} + \alpha R(x_{{p}}) + \beta U(x_{{c}}) \\&s.t. \quad x \in D\end{split}\end{equation}$$
with $$$F$$$ a nonlinear operator [8] mapping all unknowns $$$x$$$ to the sorted $$$k$$$-space data $$$\widetilde{Y}$$$. $$$N_{{R}}$$$, $$$N_{{C}}$$$ are the numbers of respiration, cardiac phases respectively. $$$x_{{p}}$$$ contains steady-state signal $$$M_{ss}$$$, equilibrium signal $$$M_{0}$$$ and effective relaxation rate $$$R_{1}^{*}$$$ of each motion state, $$$x_{{c}}$$$ is the set of corresponding coil sensitivity maps. $$$R(\cdot)$$$ is the regularization on the parameter maps:$$\begin{equation}R(x_{{p}}) = \|Wx_{{p}}\|_1 + \|x_{p}^{R}\|_{\text{TV}} + \|x_{p}^{C}\|_{\text{TV}}\end{equation}$$ with $$$\|Wx_{{p}}\|_1$$$ the joint $$$\ell_{1}$$$-Wavelet spatial regularization, $$$\|x_{p}^{R}\|_{\text{TV}}$$$ and $$$\|x_{p}^{C}\|_{\text{TV}}$$$ the temporal total variation (TV) regularization [11] along the respiration and cardiac dimensions, respectively. $$$U({\cdot})$$$ represents the Sobolev norm enforcing the smoothness of coil sensitivity maps. $$$\alpha$$$ and $$$\beta$$$ are the regularization parameters for parameter and coil sensitivity maps, respectively. $$$D$$$ is a convex set ensuring $$${R^{*}_{1}}$$$ to be nonnegative.
Similar to [8,9], the above nonlinear inverse problem is solved by the IRGNM algorithm. To enable multiple regularizations, the ADMM algorithm [12] is employed to solve the linearized subproblem in each Gauss-Newton step.
Data Acquisition
All MRI experiments were performed on a Magnetom Skyra 3T (Siemens Healthineers, Erlangen, Germany). Combined thorax and spine coils with 26 channels were utilized for all scans. Phantom measurements were performed with simulated respiration and cardiac signals (respiration cycle: 3 second, heart rate: 60 bpm). The other acquisition parameters were: FOV: $$$256 \times 256$$$ mm$$$^{2}$$$, matrix size: $$$192 \times 192$$$, slice thickness 6 mm, TR/TE = 3.27/1.98 ms, bandwidth 810 Hz/pixel. All in-vivo measurements were acquired using the nominal flip angle $$$6^{\circ}$$$ and repeated twice. All data processing was done offline and implemented in BART [13].
Results
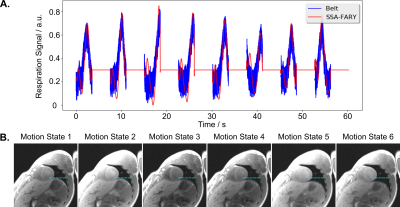
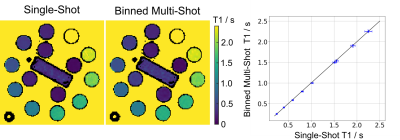
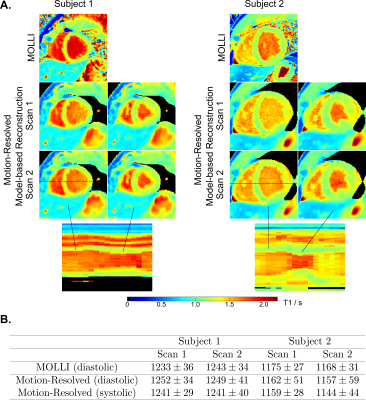
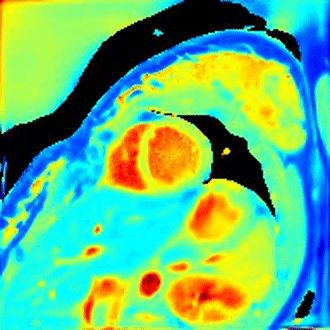
Fig 2A shows an extracted respiration signal against the respiration belt signal. The corresponding bin images of 6 respiratory motion states are presented in Fig 2B. The clearly motion-resolved motion images suggest that the adapted SSA-FARY technique could resolve respiratory motion. Fig 3 compares single-shot phantom T1 map [9] and the multi-shot T1 map estimated by motion-resolved model-based reconstruction. Visual inspection reveals good agreement between these two T1 maps. This finding is further confirmed by the quantitative ROI-analysed T1 values shown in Fig 3 (right). Fig 4A depicts MOLLI T1 map (mid-diastolic) and two representative motion-resolved T1 maps (mid-diastolic and mid-systolic) for two repetitive scans and two subjects. The line profiles along the motion dimension are shown in the bottom. The small visual difference between the repetitive scans demonstrates good intra-subject reproducibility of the proposed method, which is again confirmed by the quantitative results in Fig 4B. Additionally, myocardial T1 values of the proposed method are also in a similar range as MOLLI. Note the lateral area of the T1 map from the second subject is slightly blurred which may due to an inaccurate cardiac motion estimation. Finally, Fig 5 presents a dynamic T1 mapping example at the end-expiration state for subject 1.Discussion and Conclusion
This work develops a free-breathing myocardial T1 mapping technique using a free-running inversion-recovery radial FLASH sequence and a motion-resolved model-based reconstruction. Initial results on an experimental phantom and two healthy subjects have demonstrated good accuracy, precision and reproducibility of the proposed method. However, the present work is limited in the number of subjects and imperfect motion estimation. Further investigation and more clinical validations of the proposed method will be explored in future studies.Acknowledgements
Supported by the DZHK (German Centre for Cardiovascular Research).References
1. Moon JC, Messroghli DR, Kellman P, Piechnik SK, Robson MD, Ugander M, Gatehouse PD, Arai AE, Friedrich MG, Neubauer S, et al. Myocardial T1 mapping and extracellular volume quantification: a society for cardiovascular magnetic resonance (SCMR) and CMR working group of the european society of cardiology consensus statement. J Cardiovasc Magn Reson. 2013;15:92.
2. Kellman P, Hansen MS. T1-mapping in the heart: accuracy and precision. J Cardiovasc Magn Reson. 2014;16:2.
3. Christodoulou AG, Shaw JL, Nguyen C, Yang Q, Xie Y, Wang N, Li D. Magnetic resonance multitasking for motion-resolved quantitative cardiovascular imaging. Nat Biomed Eng. 2018;2:215.
4. Qi H, Jaubert O, Bustin A, et al. Free‐running 3D whole heart myocardial T1 mapping with isotropic spatial resolution. Magn Reson Med. 2019; 82: 1331‐1342.
5. Messroghli DR, Radjenovic A, Kozerke S, Higgins DM, Sivananthan MU, Ridgway JP. Modified look-locker inversion recovery (MOLLI) for high-resolution T1 mapping of the heart. Magn Reson Med. 2004;52:141–6.
6. Chow K, Flewitt JA, Green JD, Pagano JJ, Friedrich MG, Thompson RB. Saturation recovery single‐shot acquisition (SASHA) for myocardial T1 mapping. Magn Reson Med. 2014; 71: 2082‐2095.
7. Becker KM, Schulz-Menger J, Schaeffter T, Kolbitsch C. Simultaneous high-resolution cardiac T1 mapping and cine imaging using model-based iterative image reconstruction. Magn Reson Med. 2019;81:1080–91.
8. Wang X, Roeloffs V, Klosowski J, Tan Z, Voit D, Uecker M, Frahm J. Model-based T1 mapping with sparsity constraints using single-shot inversion-recovery radial FLASH. Magn Reson Med. 2018;79:730–40.
9. Wang, X., Kohler, F., Unterberg-Buchwald, C. et al. Model-based myocardial T1 mapping with sparsity constraints using single-shot inversion-recovery radial FLASH cardiovascular magnetic resonance. J Cardiovasc Magn Reson 21, 60 (2019) doi:10.1186/s12968-019-0570-3.
10. Rosenzweig S, Scholand N, Holme C., Uecker M. Cardiac and Respiratory Self-Gating in Radial MRI using an Adapted Singular Spectrum Analysis (SSA-FARY). IEEE Transactions on Medical Imaging. 2020;39:3029-3041.
11. Feng L, Axel L, Chandarana H, Block KT, Sodickson DK, Otazo R. XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing. Magn Reson Med. 2016;75:775–88.
12. Boyd S., Parikh N., Chu E., Peleato B., and Eckstein J. Distributed Optimization and Statistical Learning via the Alternating Direction Method ofMultipliers. Found. Trends Mach. Learn., 3(1):1–122, 2011.
13. Uecker et al., "BART Toolbox for Computational Magnetic Resonance Imaging", Zenodo, DOI: 10.5281/zenodo.592960.
Figures