3419
Estimating the pore size in a biomimetic phantom using free gradient waveforms1Cardiff University Brain Research Imaging Centre (CUBRIC), School of Psychology, Cardiff University, Cardiff, United Kingdom, 2AGH University of Science and Technology, Kraków, Poland, 3LPI, ETSI Telecomunicación, Universidad de Valladolid,, Valladolid, Spain, 4Biomedical Engineering, Case Western Reserve University, Cleveland, OH, United States, 5Department of Applied Mathematics and Computer Science, Technical University of Denmark,, Kongens Lyngby, Denmark, 6Signal Processing Lab (LTS5), École polytechnique fédérale de Lausanne (EPFL), Lausanne, Swaziland
Synopsis
Diffusion magnetic resonance imaging is a non-invasive tool to probe the microstructural features of a sample. One of these properties is the restriction size that can be measured by changing the diffusion time or alternatively changing the frequency content of the gradient waveform. B-tensor encoding was proposed recently to disentangle microstructural features of the tissue. Here we use the combination of linear, planar, and spherical tensor encoding to estimate the pore size in a biomimetic phantom, for which ground truth size estimates were available. The results show a good agreement between the estimated sizes and ground truth values.
Introduction
There are several approaches for estimating axon diameters and densities using diffusion magnetic resonance imaging (dMRI). Most of these methods use a pulsed gradient spin echo (PGSE). Stanisz et al.1 proposed a multi-compartment model to describe bovine optic nerve tissue as a combination of axons, glial cells, and extracellular space. Another model is AxCaliber which separates the diffusion-weighted signal into a two-compartment model (hindered and restricted) 2 similarly to the composite hindered and restricted model of diffusion (CHARMED) 3. Fan et al. 4 validated the estimation of pore size on a human MRI system. The acquisition in these methods is sensitized to the size by changing the diffusion time ($$$\Delta–\delta/3$$$) in a PGSE experiment. Recent studies show that there is a degeneracy in the estimation of model parameters in a two-compartment model even when the axon diameter is assumed zero (stick model) 5. B-tensor encoding 6 was proposed to mitigate this problem. In this work, we estimate the pore sizes in a biomimetic phantom 7 that has sizes (~5 um) larger than the resolution limit of clinical scanners (~3.4 um) 8 using a combination of linear, planar, and spherical tensor encoding (LTE, PTE, and STE). An important feature of this phantom is that it has an extracellular compartment which makes it interesting for the study of multi-compartment models.Theory
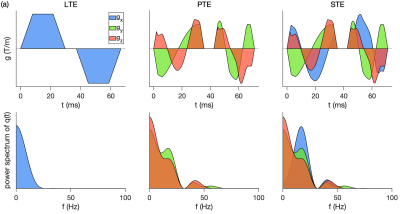
In this work, we use a two-compartment model (cylinder + ball) for the orientationally averaged diffusion-weighted signal 9-12 $$S/S_0 = f_c A_c(D_c^{\mid\mid}, D_c^\perp) + f_b A_b(D_b), \ \ \ f_c + f_b = 1$$where $$$f_c$$$and $$$f_b$$$ are the signal fractions of cylinder and ball respectively $$$A_c$$$ and $$$A_b$$$ are the signal attenuation form the cylinder and ball compartments, $$$D_c^{\mid\mid}$$$ and $$$D_c^\perp$$$ are the parallel and perpendicular diffusivity inside the cylinder and $$$D_b$$$ is the diffusivity of the ball compartment. $$$D_c^\perp$$$ is time-dependent and therefore it is a function of the cylinder radius ($$$R_c$$$). For free gradient waveforms, the diffusion time is ill-defined 9-12. We therefore consider the diffusion spectrum 9-12 in our analyses of compartment size.Method
The acquisition protocol includes one b=0 and 8 non-zero shells (b=1, 2, 3, 4.5, 6, 7.5, 9, 10.5 $$$ms/mm^2$$$) in (10, 31, 31, 31, 31, 61, 61, 61, 61) directions for LTE and 5 shells (b=1, 2, 3, 4.5, 6 $$$ms/mm^2$$$) in (31, 31, 31, 31, 61) directions for PTE and 5 shells for STE (b=0.2, 1, 2, 3, 4.5 $$$ms/mm^2$$$) in (6, 9, 9, 12, 15) directions. The 61 and 31 directions were optimized based on \citep{knutsson2018towards}. We performed our experiment on a biomimetic phantom cite[]. This includes six tubes with one (#1, #5, and #6) or two blocks of ~24 fiber layers into a tube filled with deionized water. The tube in the center is filled with free water and labeled as 0. Tube #1 and #6 had fibers with crossing angles of 45 and 90 degrees respectively, #2 and #3 randomly oriented and fibers in #4 and #5 were axially aligned.Phantom imaging: Diffusion-weighted images were acquired with the protocol detailed above on a 3T Connectom MR imaging system with 300 mT/m gradients (Siemens Healthineers, Erlangen, Germany). 30 coronal slices with 1.5 mm isotropic voxel size and a 70x70 matrix size, TE = 94 ms, TR = 4000 ms, partial Fourier factor = 6/8, and heat dissipation limit = 1, were obtained. The total acquisition time was around one hour.
Results
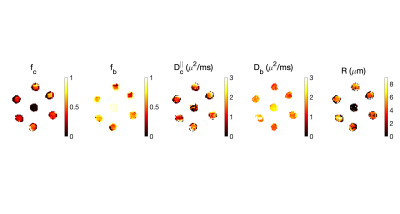
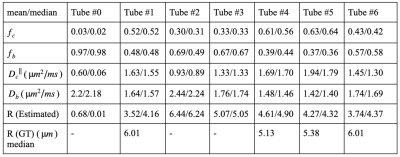
Fig. 1. shows the gradient waveforms used in this study with the corresponding frequency spectra. Fig. 2 shows the estimated parameters of the two-compartment model for different tubes of the phantom.Fig. 3 shows the mean and median of the estimated parameters in each tube. In tube #0, there is no microstructure so we expect a ball compartment with the diffusivity of the free water ($$$2.2 \mu m^2/ms$$$) at room temperature which is consistent with our findings. The median values found in tube #1, #5, and #6 are slightly lower than the ground truth values from electron microscopy. The reason can be that the effect of Rician bias is not included in our analysis.Discussion and Conclusion
In conclusion we estimated the pore size in a biomimetic phantom with ground truth values around 5 um on average for each tube. The estimated cylinder radii are in line with the ones reported from electron microscopy. We also estimated the diffusivity and the signal fraction of the cylinder and ball compartment without considering any tortuosity constraint. So we are able to separate out the two compartments and their corresponding diffusivities.Acknowledgements
The data were acquired at the UK National Facility for In Vivo MR Imaging of Human Tissue Microstructure funded by the EPSRC (grant EP/M029778/1), and The Wolfson Foundation. MA and DKJ are supported by a Wellcome Trust Investigator Award (096646/Z/11/Z) and a Wellcome Trust Strategic Award (104943/Z/14/Z). Tomasz Pieciak acknowledges the Polish National Agency for Academic Exchange for grant PN/BEK/2019/1/00421 under the Bekker programme and the Ministry of Science and Higher Education (Poland) under the scholarship for outstanding young scientists. The authors would like to thank Filip Szczepankiewicz and Markus Nilsson for providing the pulse sequences for b-tensor encoding. We also thank Markus Nilsson for the fruitful discussion about the size estimation in the frequency domain. Marco Pizzolato acknowledges the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 75446.References
[1] Stanisz, Greg J., et al. "An analytical model of restricted diffusion in bovine optic nerve." Magnetic Resonance in Medicine 37.1 (1997): 103-111.
[2] Assaf, Yaniv, et al. "AxCaliber: a method for measuring axon diameter distribution from diffusion MRI." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 59.6 (2008): 1347-1354.
[3] Assaf, Yaniv, and Peter J. Basser. "Composite hindered and restricted model of diffusion (CHARMED) MR imaging of the human brain." Neuroimage 27.1 (2005): 48-58.
[4] Fan, Qiuyun, et al. "Validation of diffusion MRI estimates of compartment size and volume fraction in a biomimetic brain phantom using a human MRI scanner with 300 mT/m maximum gradient strength." Neuroimage 182 (2018): 469-478.
[5] Jelescu, Ileana O., et al. "Degeneracy in model parameter estimation for multi‐compartmental diffusion in neuronal tissue." NMR in Biomedicine 29.1 (2016): 33-47.
[6] Westin, Carl-Fredrik, et al. "Q-space trajectory imaging for multidimensional diffusion MRI of the human brain." Neuroimage 135 (2016): 345-362.
[7] Hubbard, Penny L., et al. "Biomimetic phantom for the validation of diffusion magnetic resonance imaging." Magnetic resonance in medicine 73.1 (2015): 299-305.
[8] Nilsson, Markus, et al. "Resolution limit of cylinder diameter estimation by diffusion MRI: The impact of gradient waveform and orientation dispersion." NMR in Biomedicine 30.7 (2017): e3711.
[9] Stepišnik, Janez. "Time-dependent self-diffusion by NMR spin-echo." Physica B: Condensed Matter 183.4 (1993): 343-350.
[10] Lundell, H., et al. "Multidimensional diffusion MRI with spectrally modulated gradients reveals unprecedented microstructural detail." Scientific reports 9.1 (2019): 1-12.
[11] Afzali, Maryam, et al. "SPHERIOUSLY? The challenges of estimating spherical pore size non-invasively in the human brain from diffusion MRI." bioRxiv (2020).
[12] Lampinen, Björn, et al. "Towards unconstrained compartment modeling in white matter using diffusion‐relaxation MRI with tensor‐valued diffusion encoding." Magnetic Resonance in Medicine 84.3 (2020): 1605-1623.