3079
Fast T2 Mapping with Improved Accuracy Using Memory-Efficient Low-Rank Hankel Matrix Reconstruction1Department of Electronic Science, School of Electronic Science and Engineering (National Model Microelectronics College), National Institute for Data Science in Health and Medicine, Xiamen University, Xiamen, China, 2College of Optical Science and Engineering, Zhejiang University, Hangzhou, China, 3Department of Radiology, Mayo Clinic, Rochester, MN, United States, 4Neusoft Medical System, Shanghai, China, 5School of Computer and Information Engineering, Fujian Provincial University Key Laboratory of Internet of Things Application Technology, Xiamen University of Technology, Xiamen, China
Synopsis
Being the state-of-the-art parallel magnetic resonance imaging methods other than the deep learning approaches, the low-rank Hankel approaches embrace the advantage of holding low reconstruction errors. However, they demand intensive computations and high memory consumptions, thereby result in long reconstruction time. We proposed a new strategy for exploiting the low rankness and applied it to accelerate 2D imaging and T2 mapping. It is shown that the proposed method outperforms the state-of-the-art approaches in terms of lower reconstruction errors and more accurate mapping estimations. Besides, the proposed method required much less computation and memory consumption.
Introduction
Partial magnetic resonance imaging (MRI) to accelerate scan time has been a hot research field 1. One critical issue in this area is to recover the artifact-free image from a small subset of acquired data. Recently, approaches taking advantage of the low rankness of MRI data have been shown to provide promising reconstructions with low reconstruction errors 2-5. However, these approaches need to arrange the MRI data into a large-scale low-rank Hankel matrix. This results in high computation demands and large memory consumption, leading to slow reconstruction time. In this work, we propose a new strategy aiming to alleviate this problem and meanwhile to provide better reconstructions. We proposed to simultaneously enforce the low rankness of a series of small-size Hankel matrices, avoiding constructing the large-scale low-rank Hankel matrix thereby enables much less memory cost and allows faster computation. Particularly, the proposed methods permit effective utilization of the low-rank property as the existing low-rank Hankel methods do. We validate the proposed approaches in accelerating 2D imaging and T2 mapping.Method
Unlike the existing low-rank approaches needing to arrange large-scale Hankel matrices, we propose to simultaneously enforce the low rank of small-size Hankel matrices. The Hankel matrix size is significantly reduced allowing much less computation and memory consumption thus enables faster reconstruction time. Notably, the proposed method has lower reconstruction errors than other state-of-the-art approaches.We proposed to solve the parallel MRI reconstruction problem as
$$\mathop{\min }\limits_{\bf{X}} \sum\limits_{m=1}^M {{{\left\| {{{{\bf{\tilde{H}}}}_{{\rm{vc}}}}{\bf{\tilde{W}}}{{{\bf{\tilde{F}}}}^{{\rm{1D}}}}{{\bf{P}}_m}{\bf{X}}} \right\|}_*}}+\sum\limits_{n=1}^N{{{\left\|{{{{\bf{\tilde{H}}}}_{{\rm{vc}}}}{\bf{\tilde{W}}}{{{\bf{\tilde{F}}}}^{1{\rm{D}}}}{{\bf{Q}}_n}{\bf{X}}} \right\|}_*}} +\frac{\lambda}{2}\left\|{{\bf{Y}}-{\bf{U}}{{\bf{F}}^{{\rm{2D}}}}{\bf{X}}}\right\|_F^2+\frac{{{\lambda_1}}}{2}\left\|{{\bf{X}}-{\bf{GX}}}\right\|_F^2,$$ where the $$${\bf{X}}\in{{\mathbb{C}}^{M\times{N}\times{J}}}$$$ denotes the desired multi-coil image, $$$M$$$, $$$N$$$, and $$$J$$$ are the number of the row, column, and coils, $$${\bf{P}}_m$$$ and $$${\bf{Q}}_n$$$ denote the operators that extract $$$m$$$-th row and $$$n$$$-th column of all coil from $$$\bf{X}$$$ for $$$m=1, \cdot, M$$$, and $$$n=1,\cdot,N$$$, i.e., define $$${\bf{x}}_{m,j}^{{\rm{row}}}$$$ as the vector of $$$m$$$-th row and the $$$j$$$-th coil, and $$${\bf{x}}_{n,j}^{{\rm{col}}}$$$ as the vector of $$$n$$$-th column and the $$$j$$$-th coil. We have, $$${{\bf{P}}_m}{\bf{X}} = \left[{\begin{array}{*{20}{c}}{{\bf{x}}_{m,1}^{{\rm{row}}}}& \cdots &{{\bf{x}}_{m,j}^{{\rm{row}}}}& \cdots &{{\bf{x}}_{m,J}^{{\rm{row}}}} \end{array}}\right]\in {{\mathbb{C}}^{N \times{J}}}$$$ and $$${{\bf{Q}}_n}{\bf{X}}=\left[ {\begin{array}{*{20}{c}} {{\bf{x}}_{n,1}^{{\rm{col}}}}& \cdots &{{\bf{x}}_{n,j}^{{\rm{col}}}}& \cdots &{{\bf{x}}_{n,J}^{{\rm{col}}}} \end{array}} \right]\in{\mathbb{C}^{M\times{J}}}$$$. The operator $$${{\bf{\tilde H}}_{vc}}$$$ is defined as $$${{\bf{\tilde H}}_{{\rm{vc}}}}{\bf{\tilde W}}{{\bf{\tilde F}}^{{\rm{1D}}}}{{\bf{P}}_m}{\bf{X}} = \left[ {\begin{array}{*{20}{c}} {{\bf{HW}}{{\bf{F}}^{{\rm{1D}}}}{\bf{x}}_{m,1}^{{\rm{row}}}}& \cdots &{{\bf{HW}}{{\bf{F}}^{{\rm{1D}}}}{\bf{x}}_{m,J}^{{\rm{row}}}}&{{\bf{HW}}{{\bf{F}}^{{\rm{1D}}}}{{\left( {{\bf{x}}_{m,1}^{{\rm{row}}}} \right)}^{\dagger} }}& \cdots &{{\bf{HW}}{{\bf{F}}^{{\rm{1D}}}}{{\left( {{\bf{x}}_{m,J}^{{\rm{row}}}} \right)}^{\dagger} }} \end{array}} \right]$$$, where $$${\dagger}$$$ denotes conjugating and reflecting around the zero-frequency, $$$\bf{H}$$$ denotes the operator converting a vector to a Hankel matrix, $$$\bf{F}^{\rm{1D}}$$$ the 1D Fourier transform, $$$\bf{W}$$$ the weighting matrix. $$$\bf{Y}$$$ is the acquired multi-coil k-space data with zero-filling in unacquired position, $$$\bf{F}^{\rm{2D}}$$$ the 2D Fourier transform, $$$\bf{U}$$$ the undersampling matrix, and $$$\bf{G}$$$ the SPIRiT operator matrix in the image domain.
We also applied the memory-efficient low-rank Hankel matrix approach to T2 mapping reconstruction. Denote the desired T2 mapping image $$${\bf{X}}\in{\mathbb{C}^{M\times{N}\times{L}\times{J}}}$$$, $$$L$$$ and $$$J$$$ are the number of echoes and coils, $$$M$$$ and $$$N$$$ are the number points in the readout and phase encoding dimensions, respectively. We reconstructed the y-t plane image $$${\bf{X}}_m^{{\rm{y-t}}} \in {\mathbb{C}^{N\times{L}\times{J}}}$$$ along the readout dimension one by one with the reconstruction problem: $$\mathop {\min }\limits_{{\bf{X}}_m^{{\rm{y-t}}}} \sum\limits_{n=1}^N {{{\left\| {{\bf{\tilde H}}{{\bf{P}}_n}{\bf{X}}_m^{{\rm{y-t}}}} \right\|}_*}}+{\lambda _2}\sum\limits_{l=1}^L{{{\left\| {{{{\bf{\tilde{H}}}}_{{\rm{vc}}}}{\bf{\tilde W}}{{{\bf{\tilde F}}}^{1{\rm{D}}}}{{\bf{Q}}_l}{\bf{X}}_m^{{\rm{y-t}}}} \right\|}_*}}+\frac{\lambda }{2}\left\| {{\bf{Y}}_m^{{\rm{y-t}}}-{\bf{U}}{{\bf{F}}^{{\rm{1D}}}}{\bf{X}}_m^{{\rm{y-t}}}} \right\|_F^2,$$
where $$${\bf{Y}}_{m}^{\rm{y-t}}$$$ denotes the acquired k-space data of $$$m$$$-th y-t plane (inverse Fourier transform has been done in the readout dimension).
Results
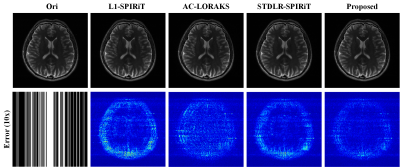
1. Accelerate 2D imagingAs shown in Fig. 1, the proposed approach produces an image with the lowest error. The errors inside the skull are uniform and very small compared to the competing results. Besides, the computational time of $$$\ell_1$$$-SPIRiT 6, AC-LORAKS 7, STDLR-SPIRiT 5, and the proposed method are 22.5 seconds, 7.4 seconds, 1090.3 seconds, and 80.3seconds, respectively. Overall, the results demonstrate the promising performance and relatively fast reconstruction speed of the proposed method, e.g., a more than 12 times acceleration was obtained by the proposed when compared to the structured low-rank method, STDLR-SPIRiT.
2. Accelerate T2 mapping
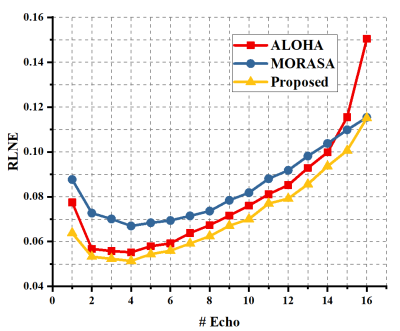
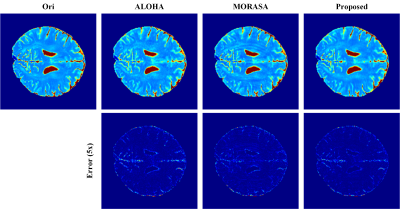
We performed reconstruction on brain T2 mapping (16 echoes) using 1D Cartesian with partial Fourier sampling pattern. As shown in Fig. 2, the proposed approach permits the lowest RLNEs for all 16 images than the state-of-the-art approaches. The estimated T2 map of the proposed method also enables the lowest error (Fig. 3), indicating the proposed approach can provide more accurate quantitative results than other state-of-the-art methods. Besides, the proposed method reconstructed all echo images with the fastest speed using only 197 seconds, while ALOHA 9 used 309 seconds and MORASA 8 cost 1200 seconds.
Conclusion
We present a new strategy for enforcing the low-rankness of parallel MRI data to achieve lower computations and memory consumption and also provide promising results. We validated the idea in both spatial encoding MRI and T2 mapping problems. In both cases, the proposed approaches outperform the state-of-the-art methods in terms of lower errors and reduced computational time significantly compared to a majority of low-rank Hankel approaches.Acknowledgements
This work was supported in part by the National Key R&D Program of China (2017YFC0108703), National Natural Science Foundation of China (61971361, 61871341, 61811530021, U1632274), Natural Science Foundation of Fujian Province of China (2018J06018), Fundamental Research Funds for the Central Universities (20720180056), and Xiamen University Nanqiang Outstanding Talents Program.
The correspondence should be sent to Dr. Xiaobo Qu (Email: quxiaobo@xmu.edu.cn).
References
[1] M. Lustig, D. Donoho, and J. M. Pauly, "Sparse MRI: The application of compressed sensing for rapid MR imaging," Magnetic Resonance in Medicine, vol. 58, no. 6, pp. 1182-1195, 2007.
[2] K. Jin et al., "A general framework for compressed sensing and parallel MRI using annihilating filter based low-rank Hankel matrix," IEEE Transactions on Computational Imaging, vol. 2, no. 4, pp. 480-495, 2016.
[3] J. P. Haldar, "Low-rank modeling of local k-space neighborhoods (LORAKS) for constrained MRI," IEEE Transaction on Medical Imaging, vol. 33, no. 3, pp. 668-81, 2014.
[4] G. Ongie and M. Jacob, "Off-the-grid recovery of piecewise constant images from few Fourier samples," SIAM Journal on Imaging Sciences, vol. 9, no. 3, pp. 1004-1041, 2016.
[5] X. Zhang et al., "Image reconstruction with low-rankness and self-consistency of k-space data in parallel MRI," Medical Image Analysis, vol. 63, 101687, 2020.
[6] M. Lustig and J. M. Pauly, "SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space," Magnetic Resonance in Medicine, vol. 64, no. 2, pp. 457-71, 2010.
[7] J. P. Haldar, "Autocalibrated LORAKS for fast constrained MRI reconstruction," in 2015 IEEE 12th International Symposium on Biomedical Imaging (ISBI), 2015, pp. 910-913.
[8] D. Lee, K. H. Jin, E. Y. Kim, S. H. Park, and J. C. Ye, "Acceleration of MR parameter mapping using annihilating filter-based low rank Hankel matrix (ALOHA)," Magnetic Resonance in Medicine, vol. 76, no. 6, pp. 1848-1864, 2016.
[9] X. Peng, L. Ying, Y. Liu, J. Yuan, X. Liu, and D. Liang, "Accelerated exponential parameterization of T2 relaxation with model-driven low rank and sparsity priors (MORASA)," Magnetic Resonance in Medicine, vol. 76, no. 6, pp. 1865-1878, 2016.
Figures