2664
Fully automatic extraction of mitral valve annulus motion parameters on long axis CINE CMR using deep learning1Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany, 2Magnetic Resonance, Siemens Healthcare GmbH, Erlangen, Germany
Synopsis
The analysis of mitral valve motion is known to be relevant in the diagnosis of cardiac dysfunction. Dynamic motion parameters can be extracted from Cardiac Magnetic Resonance (CMR) images. We propose two chained Convolutional Neural Networks for automatic tracking of mitral valve-annulus landmarks on time-resolved 2-chamber and 4-chamber CMR images. The first network is trained to detect the region of interest and the second to track the landmarks along the cardiac cycle. We successfully extracted several motion-related parameters with high accuracy as well as analyzed unlabeled datasets, thereby overcoming time-consuming annotation and allowing statistical analysis over large number of datasets.
Introduction
Overall prevalence of heart failure with preserved ejection fraction (HFpEF) has been reported to be 1.1–5.5 % in the general population and is typically related to diastolic dysfunction1. It is known that the analysis of the mitral valve annulus (MVA) throughout the cardiac cycle might act, amongst others, as a predictor for HFpEF2.We propose a robust, fully automated algorithm that tracks the MVA insertion points on 2-chamber (2CHV) and/or 4-chamber (4CHV), CINE CMR series. The network system initially detects the mitral valves’ region of interest (ROI) before extracting the time-resolved MVA landmarks. This information is then used to extract motion-related parameters including velocities (e’-waves) and diameters. The system performance is analyzed based on annotated data. Thereafter, motion parameters are extracted retrospectively on N=1468 unlabeled datasets3.
In recent work, atrioventricular plane tracking was shown feasible using direct coordinate regression, however, without temporal feature extraction4, in contrast to the present work.
Materials and Methods
Data: Ground-truth annotated images from 83 subjects were provided by the Cardiac Atlas Project landmark detection challenge, composed of 1.5T (99%) and 3T (1%) 2CHV and 4CHV. This multi-vendor (GE Medical Systems, Philips Medical Systems, Siemens Healthcare) data included semi-automatically annotated MVA landmarks throughout the cardiac cycle5. Mean in-plane resolution was $$$1.48\pm0.37 $$$ mm.Network System (Fig. 1): All CINE series were temporally interpolated to 32 timeframes, flipped to show the apex in an upwards orientation and split into 70% training, 15% validation and 15% testing data subsets. The algorithm consists of two chained CNNs, both trained to detect landmarks based on a heatmap regression task6. The first network (Localization CNN) is a Residual 2D UNet7 model identifying the MVA ROI in both, 4CHV or 2CHV by regressing three landmarks on the first timeframe of each series. After rotation cropping and 0.5 mm pixel space interpolation, a 3D UNet8, the second network (Landmarks CNN) extracts time-resolved heatmaps of both landmarks. A post-processing step fits a Gaussian to refine the final landmark coordinates.
Training: The model (Fig. 2) was trained from scratch using the Adaptive Wing Loss9 on the heatmaps while decreasing the heatmaps standard deviation10 exponentially throughout training epochs $$$ σ_{ep}=16 \cdot 0.95^{ep} $$$. The networks were trained using Adam optimizer11 with momentum of $$$\beta=0.9$$$ and learning rate $$$\lambda=0.0001$$$ with weight decay regularization. Online data augmentation was performed using random rotation, contrast enhancement, translation, maximum clipping, blurring and noise addition.
Parameter Extraction: Time-resolved motion curves were extracted from the CNN and the following derived parameters calculated (Fig. 3):
- MVA plane displacement (MVAPD) curve was defined as the time-resolved perpendicular distance of the MVA plane relative to the first frame. Peak displacement (MVAPD-PD) was also extracted4,12.
- MVA plane velocity (MVAPV) was derived as the MVAPD time-resolved discrete temporal derivate4,12. Early diastolic velocity (MVAPV-e´) was then defined as the central maximum of the MVAPV.
- The total motion of the annulus (VAD) was quantified as the total displacement sum over all timeframes in mm.
- The septal and lateral MVA landmark velocity curves (SMVAV, LMVAV) were computed as the temporal derivative of each landmark displacement 13. The central maximum of each curve represents early annular diastolic velocity (MAVL-e’).
- The time-resolved diameter evolution throughout the cardiac cycle was derived as the Euclidean distance between landmarks in mm and the maximum diameter14 (MAMD) as well as the difference between maximum and minimum diameter (MADC) were extracted6.
Results
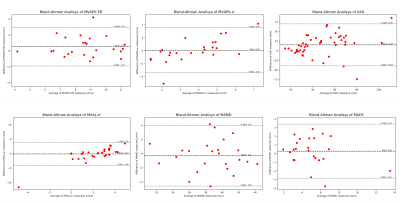
Landmark coordinate mean errors of $$$1.75 \pm 0.64 $$$ (2CHV) and $$$ 1.74 \pm 0.72$$$ 4CHV, were achieved.Bland-Altman analysis revealed following mean agreement values (Fig. 4) : MVAPD-PD: $$$0.51\pm2.42 $$$ mm, MVAPV-e´: $$$0.08\pm2.44 $$$ cm/s, VAD: $$$15.39\pm54.62$$$ mm and for MAVL-e’ $$$0.08 \pm3.73$$$ cm/s; MAMD: $$$0.31\pm3.66$$$ mm and MADC $$$0.28\pm3.12$$$ mm.
The localization network fails to locate the ROI in less than $$$0.5\%$$$ of unlabeled datasets and at least one time-frame was not smoothly tracked in $$$16.53\%$$$ of unlabeled series.
Discussion and Conclusion
The proposed system was shown to successfully track MVA landmarks with a mean error in the range of the data’s resolution. Extraction of derived parameters of interest was successful and showed good agreement with ground-truth data, based on Bland-Altman analysis. Heatmap regression avoids the need to learn the highly non-linear domain transfer, from pixel to coordinate space which might explain the high accuracy with a comparatively small annotated dataset size (N=83).Future work will include on-line integration of the approach and analysis of motion parameters on larger numbers of categorized patient datasets. Furthermore, a prospective slice-tracking CMR acquisition is planned for improved morphological and/or flow measurements of the mitral valve15.
Acknowledgements
No acknowledgement found.References
1.Oktay, A Afşin et al. “The emerging epidemic of heart failure with preserved ejection fraction.” Current heart failure reports vol. 10,4 (2013): 401-10. doi:10.1007/s11897-013-0155-7
2. Ramos, João G et al. “Comprehensive Cardiovascular Magnetic Resonance Diastolic Dysfunction Grading Shows Very Good Agreement Compared With Echocardiography.” JACC. Cardiovascular imaging vol. 13,12 (2020): 2530-2542. doi:10.1016/j.jcmg.2020.06.027
3. Sudlow, Cathie et al. “UK biobank: an open access resource for identifying the causes of a wide range of complex diseases of middle and old age.” PLoS medicine vol. 12,3 e1001779. 31 Mar. 2015, doi:10.1371/journal.pmed.1001779
4.Gonzales Ricardo A et. al.Time-resolved tracking of the atrioventricular plane displacement in long-axis cine images with residual neural networks. Proceedings of the Joint Annual Meeting ISMRM-ESMRMB (28th Annual Meeting & Exhibition) (2020)
5.Fonseca, Carissa G et al. “The Cardiac Atlas Project--an imaging database for computational modeling and statistical atlases of the heart.” Bioinformatics (Oxford, England) vol. 27,16 (2011): 2288-95. doi:10.1093/bioinformatics/btr360
6. Payer, Christian et al. “Integrating spatial configuration into heatmap regression based CNNs for landmark localization.” Medical image analysis vol. 54 (2019): 207-219. doi:10.1016/j.media.2019.03.007 7. Ronneberger, Olaf, et al. U-net: Convolutional networks for biomedical image segmentation. International Conference on Medical image computing and computer-assisted intervention. Springer, Cham, 2015.
8. Özgün Çiçek, et. al. 3D U-Net: Learning Dense Volumetric Segmentation from Sparse Annotation. CoRR abs/1606.06650 (2016)
9. Xinyao Wang et. al., L. Bo and L. Fuxin, "Adaptive Wing Loss for Robust Face Alignment via Heatmap Regression," 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea (South), 2019, pp. 6970-6980, doi: 10.1109/ICCV.2019.00707.
10.Teixeira, Brian et al. “Adaloss: Adaptive Loss Function for Landmark Localization.” ArXiv abs/1908.01070 (2019).
11. Kingma, Diederik P., et al. (2014). Adam: A Method for Stochastic Optimization. International Conference on Learning Representations .arXiv preprint arXiv:1412.6980 (2014).
12. Seemann, F. et al. “Time-resolved tracking of the atrioventricular plane displacement in Cardiovascular Magnetic Resonance (CMR) images.” BMC Medical Imaging 17 (2017):
13.Thavendiranathan, P. et al. “Mitral annular velocity measurement with cardiac magnetic resonance imaging using a novel annular tracking algorithm: Validation against echocardiography.” Magnetic resonance imaging 55 (2019): 72-80 .
14. Han, Yuchi et al. “Cardiovascular magnetic resonance characterization of mitral valve prolapse.” JACC. Cardiovascular imaging vol. 1,3 (2008): 294-303. doi:10.1016/j.jcmg.2008.01.013.
15. Seemann, Felicia et al. “Valvular imaging in the era of feature-tracking: A slice-following cardiac MR sequence to measure mitral flow.” Journal of magnetic resonance imaging : JMRI vol. 51,5 (2019): 1412-1421. doi:10.1002/jmri.26971
Figures
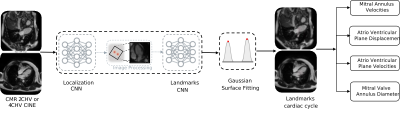
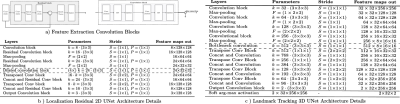
Figure 2: a) Feature extraction 2D Residual and 3D convolution
blocks. Each residual block consists of a spatial convolution(CONV)(3x3), Batch Normalization (BN) and Leaky Rectified Linear Units (LReLU)
activation layers. The 3D block consist of double spatial and temporal CONV(3x3x3)-BN-LReLU operations. b) Localization CNN architecture based on 2-D UNet with 3 encoder-decoder blocks. c) Landmark tracking Fully CNN architecture details based on 3-D UNet.For down-sampling asymmetrical max-pooling layers were applied into temporal and spatial dimensions.

Figure 3: a) Example of network output for a 2CHV and a 4CHV dataset. b) Representation of the MVA plane in systole end diastole with representation of different MVA motion parameters (MAMD, SMVAV, LMVAV, MVAPD). c-e) Mean and standard deviation of derived parameters from ground truth annotations (black) and predicted landmarks (red) for test subset (N=12) along the cardiac cycle. The error bars represent the standard deviation in each plot: c) MAVPD and corresponding MAVPV, d) SMVAV and LMVAV, e) annulus diameter.