1522
Adaptive space-filling curve for improved feature selection from fMRI brain activation maps: application to schizophrenia classification1Computer Engineering, University of Houston - Clear Lake, Houston, TX, United States, 2Computer Science, University of Houston - Clear Lake, Houston, TX, United States, 3Center for Translational Research in Neuroimaging and Data Science (TReNDS), Atlanta, GA, United States
Synopsis
In this work, we develop a 3D to 1D ordering methodology for fMRI data, using a new space filling curve (SFC), which is adaptive to brain's shape based on T1 MRI. We apply this SFC ordering to fMRI activation maps from a schizophrenia study, compress/bin the data, obtain features, and perform classification of schizophrenia vs normal controls. The classification results using SFC ordering are superior to those using linear ordering, the traditional method.
INTRODUCTION
Functional MRI (fMRI) volumes are 3 dimensional (3D) volumes (e.g.a 64×64×64 matrix), they usually need to be converted to arrays of a single dimension (1D), for further analysis (Figure 1), e.g. for regression, general linear model, independent component analysis, etc. Traditionally, a linear ordering/mapping from 3D to 1D have been used, i.e. 3D data are scanned consecutively along the first, second, third dimensions in order to obtain a 1D ordering of volumes. Linear ordering results in large "jumps" or "discontinuities" of signals, and it does not preserve the structure of the brain in 1D1. By traversing 3D volumes using a space-filling curve (SFC)2-6, which is adaptive to brain's shape, the 3D image can be ordered into 1D space (e.g. 643×1 vector for a 64×64×64 volume) which can better preserve the brain's structure in 1D1. Any dimensionality reduction, smoothing, down-sampling, compression, and feature selection or reduction in 1D can benefit from better preservation of information, when compared with linear ordering and any other pre-determined orderings such as Hilbert ordering. In this work, building on previous work which had only a 60%-complete SFC7,8, we computed an improved, 99.2%-complete SFC, adaptive to brain's shape (on a T1 MRI template image)9, used it to order fMRI activation maps from 3D to 1D in two groups of participants, schizophrenia patients (SP) and healthy controls (HC), obtained features, and performed classification of participants.METHODS AND MATERIALS
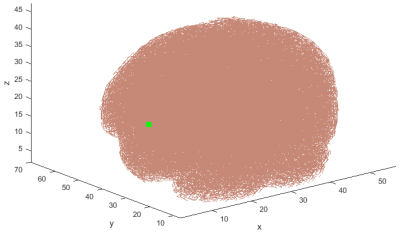
89 healthy control (HC) participants and 95 participants with schizophrenia (SP) were scanned using 3T Siemens MRI scanners at four different sites. Research protocol was reviewed and approved by the IRB of the local institutions where scans were performed. Functional data were acquired at four sites with Siemens 3T Trio scanners. Data were collected from each participant while performing a sensorimotor (SM) task. The parameters for the functional scan were: TR/TE = 2s/30ms, bandwidth = ±100 kHz = 3126 Hz/pixel, FA = 90°, slice thickness = 4 mm, gap between slices = 1 mm, voxel size = 3.4 mm × 3.4 mm × 4 mm, FOV = 22 cm, pulse sequence = PACE-enabled, single shot, single-echo echo planar imaging (EPI), scan plane = oblique axial, AC-PC; acquisition matrix = 64 × 64, number of slices = 27, ascending sequential acquisition. Participants performed a sensorimotor (SM) task during the scan. After pre-processing, and normalization to MNI space, the fMRI activation maps computed as standard parametric maps of t-value with the SM task, were resampled to 3mm×3mm×3mm standard MNI space, which resulted in 53 × 63 × 46 data matrix. An adaptive space-filling curve (SFC) using a 53 × 63 × 46 T1 MRI template in MNI space was computed using a greedy search algorithm developed in house (Figure 2).The 3D fMRI maps from each participant were converted to 1D with linear ordering (Figure 3), and with the comouted adaptive SFC (Figure 4). The 1D arrays were down-sampled by a "bin size" of 64, values were averaged across each bin ("binning", Figures 3 and 4), which resulted in 1,010 raw features. These features were used to train the classification algorithm by using a random 70% of the participants and were tested on the remaining 30%. The training and testing process was repeated 1000 times by using new random selection of training and testing datasets. Average classification accuracies were computed.RESULTS
Figure 3 shows results of linear ordered, zoomed, and binned 1D array, respectively, for a participant; and Figure 4 shows results of newly developed SFC-ordered array. Large clusters can be seen in the SFC-ordered array, whereas linear ordering resulted in a highly disconnected or unclustered brain activation signal. Using the SFC ordering, the perceptron classification algorithm10 resulted in 93.5% average accuracy in classification of SP vs HC participants, whereas the linear ordering resulted in only 59.1% classification accuracy. Superior classification performance of SFC-ordering over linear ordering persisted (86.9-88.6% vs. 59.9-60.3%) also when SVM and Random Forest algorithms were employed10. Overall, SFC-based classification results were superior. As a benchmark, doing a coarse 4×4×4 down-sampling of the brain activation maps directly in 3D, and then ordering the resulting 64×-down-sampled brain with linear ordering and using the resulting signal as features, resulted in a chance accuracy of around 50% for participant classification.DISCUSSION AND CONCLUSION
A space-filling curve (SFC) adaptive to brain's shape can be utilized to order fMRI data such as brain activation maps in fMRI analyses and it proves to be better than using the traditional linear ordering for preserving information; in our study, SFC ordering resulted in better features from the activation maps, which resulted in higher classification accuracy of two groups of participants, schizophrenia patients and healthy controls. The results need to be replicated with larger sample sizes or with other fMRI studies. Potential future work also involves using different feature reduction methods and different classification algorithms, and compression of fMRI/MRI data based on the developed SFC.Acknowledgements
UHCL graduate student Lohit Bhupati was supported by a UHCL FRSF grant to Unal Sakoglu; and UHCL undergraduate student Olexandra Petrenko was supported by an NCSI XSEDE EMPOWER grant to Unal Sakoglu.References
[1] Sakoglu U, Arslan AN, Bohra K, Flores H, "In Search of Optimal Space-Filling Curves for 3-D to1-D Mapping: Application to 3-D Brain MRI Data", Proceedings of the 6th International Conference on Bioinformatics and Computational Biology (BICOB), 61-66, March 2014, Las Vegas, NV, USA (2014).
[2] Hilbert, D.: Uber die stetige abbildung einer linie auf flachenstuck (in German). Math. Annln. 459–460 (1891).
[3] Moon, B., Jagadish, H., Faloutsos, C., Saltz, J.: Analysis of the clustering properties of the Hilbert space-filling curve. IEEE Transactions on Knowledge and Data Engineering 124–141 (2001).
[4] Kontos D, Megalooikonomou V, Ghubade N, Faloutsos C, "Detecting Discriminative Functional MRI Activation Patterns Using Space Filling Curves", Proceedings of the 25th Annual International Conference of the IEEE EMBS, 963-966, September 17-21,2003, Cancun, Mexico.
[5] Griffiths JG: An algorithm for displaying a class of space-filling curves. Software Practice and Experience 16 403–411 (1986).
[6] Wang, Q., Kontos, D., Li, G., Megalooikonomou, V.: Application of time series techniques to data mining and analysis of spatial patterns in 3d images. In: ICASSP. 525–528 (2004).
[7] Sakoglu U, Bhupati L, “Classification of fMRI Study Participants Using Space-Filling-Curve Orderings of fMRI Brain Activation Maps,” Proceedings of the International Society for Magnetic Resonance in Medicine (ISMRM) (2020).
[8] Sakoglu U, Bhupati L, Beheshti N, Tsekos N, Johnsson L, "An Adaptive Space-Filling Curve Trajectory for Ordering 3D Datasets to 1D: Application to Brain MRI Data for Classification," Lecture Notes in Computational Science (LNCS), Springer, Vol. 12139, pp. 635-646 (2020).
[9] A.C. Evans, A.L. Lanke, D.L. Collins, S. Baillet, “Brain templates and atlases,” Neuroimage, vol. 62, pp 911-922 (2010).
[10] Alpaydin, E., Introduction to Machine Learning, 3rd Ed., MIT Press, 2020.
Figures
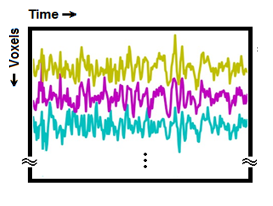
Fig. 1. Conventionally, fMRI dataset voxels are ordered using linear ordering into rows of a matrix, as a result, a matrix of voxels × time is generated for further analyses.
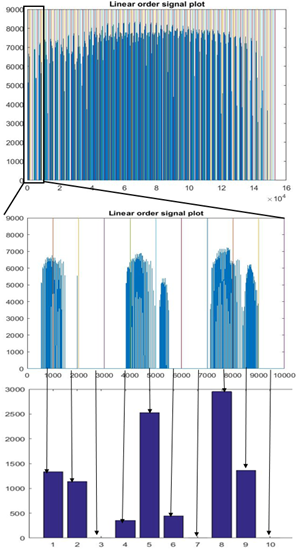
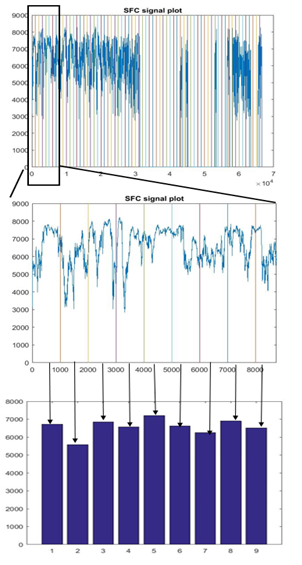
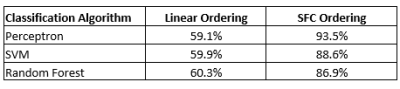
Fig. 5. Patient (n=95) vs control (n=89) classification accuracy (average across 1000 random train/test subsets) with different ordering and classification methods. SFC ordering leads to higher accuracy vs linear ordering.