0753
Free-Breathing Liver Fat and R2* Mapping: Multi-Echo Radial FLASH and Model-based Reconstruction (MERLOT)
Zhengguo Tan1,2, Sebastian Rosenzweig1,2, Xiaoqing Wang1,2, Nick Scholand1,2, H Christian M Holme1,2, Moritz Blumenthal1, and Martin Uecker1,2,3,4
1Institute for Diagnostic and Interventional Radiology, University Medical Center Göttingen, Göttingen, Germany, 2German Center for Cardiovascular Research (DZHK), Göttingen, Germany, 3Cluster of Excellence "Multiscale Bioimaging: from Molecular Machines to Networks of Excitable Cells" (MBExC), University of Göttingen, Göttingen, Germany, 4Campus Institute Data Science, University of Göttingen, Göttingen, Germany
1Institute for Diagnostic and Interventional Radiology, University Medical Center Göttingen, Göttingen, Germany, 2German Center for Cardiovascular Research (DZHK), Göttingen, Germany, 3Cluster of Excellence "Multiscale Bioimaging: from Molecular Machines to Networks of Excitable Cells" (MBExC), University of Göttingen, Göttingen, Germany, 4Campus Institute Data Science, University of Göttingen, Göttingen, Germany
Synopsis
To achieve free-breathing liver fat and $$$R_2^\star$$$ mapping, this work combines multi-echo radial FLASH with stack-of-stars volumetric acquisition and SSA-FARY to resolve respiratory motion. Moreover, regularized model-based reconstruction is implemented in BART to directly estimate quantitative parameter maps from acquired k-space data. Joint spatial and temporal regularization is used in this work. The proposed method is validated with NIST and water/fat phantoms. Furthermore, free-breathing liver studies show repeatability and good agreement between single-slice real-time and volumetric acquisition.
INTRODUCTION
The $$$T_2^\star$$$-IDEAL [1,2,3] technique relies on a pre-calibrated $$$B_0$$$ field inhomogeneity map and image-domain fitting to obtain quantitative water/fat images and $$$R_2^\star$$$ maps. Model-based reconstruction [4] has been proposed to estimate parameter maps directly from acquired k-space data and enabled higher acceleration factor in liver fat/$$$R_2^\star$$$ quantification [5,6]. These techniques, however, still require either a breath hold (~20 sec) or relatively long free-breathing scans (~4 min). To address these problems, this work extended our previously proposed multi-echo radial FLASH sequence [7] to stack-of-stars volumetric acquisition utilizing SSA-FARY [8] to resolve respiratory motion. In addition, this work leveraged advanced regularization methods implemented in BART [9] to achieve joint spatial and temporal regularization.THEORY
Multi-Echo Radial FLASHFigure 1 illustrates the multi-echo radial FLASH sequence and its corresponding $$$k$$$-space trajectory. With the blip gradients, multiple echoes (7 echoes in this work) with different radial spoke encoding are sampled per RF excitation.
Generalized Regularized Model-based Reconstruction
The independent water/fat signal sampled by multi-gradient-echo sequences is modeled as [3],
$$$B : x \mapsto \rho_m = \bigg( \text{W} \cdot e^{-{R_2^\star}_\text{W} \text{TE}_m} + \text{F} \cdot z_m \cdot e^{-{R_2^\star}_\text{F} \text{TE}_m} \bigg) \cdot e^{i2\pi f_{B_0} \text{TE}_m}$$$ with $$$x = (\text{W}, {R_2^\star}_\text{W}, \text{F}, {R_2^\star}_\text{F}, f_{B_0})^T$$$.
$$$\rho_m$$$ denotes the $$$m$$$th echo signal. $$$\text{W}$$$ and $$$\text{F}$$$ are the water and fat proton density, respectively. Plus, water and fat have their independent $$$R_2^\star$$$ relaxation rate. The fat chemical-shift-induced phase modulation is $$$z_m = \sum_p a_p \cdot e^{i2\pi f_p \text{TE}_m}$$$ with $$$f_p$$$ being the 6-peak fat spectrum with their corresponding amplitude $$$a_p$$$ [10]. The last term is the $$$B_0$$$ field inhomogeneity ($$$f_{B_0}$$$) induced phase modulation. Noteworthy, this model can be reduced to the well-known single $$$R_2^\star$$$ model when assuming water and fat share the same $$$R_2^\star$$$ [1,2] or in the presence of only water. The nonlinear model is then combined with the parallel imaging model [11] and thus $$$F_{j,m} (x) = P_m \mathcal{F} S B_m$$$, where $$$x$$$ also includes coil sensitivity maps and $$$P_m \mathcal{F}$$$ denotes the non-uniform FFT operator of the $$$m$$$th echo. To jointly estimate all unknowns, the objective function is
$$$\arg\!\min_x \left\lVert y - F(x) \right\rVert_2^2 + \alpha R(x)$$$
This regularized nonlinear inverse problem is solved by IRGNM [11] with ADMM [12], allowing generalized regularization terms. This work utilized (1) joint $$$\ell^1$$$-Wavelet spatial regularization onto the parameter maps (including $$$\text{W}$$$, $$${R_2^\star}_\text{W}$$$, $$$\text{F}$$$, $$${R_2^\star}_\text{F}$$$), (2) spatial smoothness constraint on $$$B_0$$$ field inhomogeneity and coil sensitivity maps, (3) $$$\ell^2$$$-Tikhonov regularization onto all unknowns, (4) non-negativity constraints on $$$R_2^\star$$$ maps, and (5) temporal TV regularization for dynamic acquisition [13]. This nonlinear inverse problem is initialized with the estimate from model-based 3-point water/fat separation [7], while $$$R_2^\star$$$ and coil sensitivity maps are initialized as 0. For 3D data, initialization uses an initial reconstruction that uses sequential reconstruction along the partition dimension with regularization relative to the previous partition.
METHODS
Validation StudiesBoth the NIST and a simple water/fat phantom were used for validation. The water/fat phantom consists of four tubes filled with Rama (7% fat), Kochsahne (15% fat), Schlagsahne (at least 30% fat), and peanut oil (92g fat per 100mL). The tube in the center is filled with distilled water. MERLOT was compared with reference $$$R_2^\star$$$ and fat fraction maps obtained via multi-gradient-echo Cartesian acquisition with pixel-wise fitting.
Free-Breathing Liver
Free-breathing liver studies were conducted with both 2D single-slice and 3D stack-of-stars protocols. Detailed acquisition parameters were flip angle $$$5^o$$$, FOV $$$320$$$ mm, voxel size $$$1.6 \times 1.6 \times 5.0$$$ mm$$$^3$$$, base resolution $$$200$$$, bandwidth $$$1090$$$ Hz/pixel, and 7 echoes with TEs $$$1.31, 2.54, 3.77, 5.00, 6.23, 7.46, 8.69$$$ ms and TR $$$9.89$$$ ms. For single-slice acquisition, each frame consisted of $$$33$$$ RF excitation, leading to a temporal resolution of $$$326$$$ ms per frame. For stack-of-stars acquisition [14], a total of $$$36$$$ partitions and $$$330$$$ excitation were used (i.e. total scan time of $$$1.95$$$ min).
RESULTS
Validation StudiesAs shown in Figure 2, the spatial smoothness constraint on $$$f_{B_0}$$$ avoids artifacts which appear in the pixel-wise fitting reconstruction. Quantitative analysis of the reconstructed $$$R_2^\star$$$ and fat fraction values of the selected ROIs shows good match between these two methods.
Free-Breathing Liver
Figure 3 shows reconstruction results with only spatial sparsity and with joint spatial and temporal sparsity regularization. The latter reduces noise and streaking artifacts in the reconstructed parameter maps.
Figure 4 shows motion-resolved reconstruction results via SSA-FARY and joint spatial and temporal regularization. Quantitative analysis of both single-slice and stack-of-stars acquisition in Table 1 shows overall agreement of quantitative $$$R_2^\star$$$ and fat fraction values between different acquisitions. In addition, the result from the 2nd scan shows close similarity to the 1st scan, which demonstrates the repeatability of the proposed method.
Discussion and Conlusion
This work presents free-breathing and volumetric water/fat separated $$$R_2^\star$$$ and $$$B_0$$$ field mapping of the liver based on efficient multi-echo radial FLASH acquisition and regularized model-based reconstruction (MERLOT). The method is validated via the NIST and water/fat phantom. Liver studies show that the regularization technique not only improves image quality but also accelerates free-breathing volumetric acquisition. This method might be beneficial with a standardized water/fat phantom validation, comparison with established fat/$$$R_2^\star$$$ mapping techniques, and clinical studies.Acknowledgements
The authors would like to thank funding support from DZHK (German Centre for Cardiovascular Research), DFG (German Research Foundation) under grant TA 1473/2-1 / UE 189/4-1 and under Germany’s Excellence Strategy—EXC 2067/1‐390729940, and in part by NIH under grant U24EB029240.References
- Reeder SB, Wen Z, Yu H, Pineda AR, Gold GE, Markl M, et al. Multicoil Dixon chemical species separation with an iterative least-squares estimation method. Magn Reson Med 2004;51:35-45.
- Yu H, McKenzie CA, Shimakawa A, Vu AT, Brau ACS, Beatty PJ, et al. Multiecho reconstruction for simultaneous water-fat decomposition and $$$T_2^*$$$ estimation. J Magn Reson Imaging 2007;26:1153-1161.
- Chebrolu VV, Hines CDG, Yu H, Pineda AR, Shimakawa A, McKenzie CA, et al. Independent estimation of $$$T_2^*$$$ and fat for improved accuracy of fat quantification. Magn Reson Med 2010;63:849-857.
- Block, KT, Uecker M, Frahm J. Model-based iterative reconstruction for radial fast spin-echo MRI. IEEE Trans Med Imaging 2009;28:1759-1769.
- Wiens CN, McCurdy CM, Willig-Onwuachi JD, McKenzie CA. $$$R_2^*$$$-corrected water-fat imaging using compressed sensing and parallel imaging. Magn Reson Med 2014;71:608-616.
- Schneider M, Benkert T, Solomon E, Nickel D, Fenchel M, Kiefer B, et al. Free-breathing fat and $$$R_2^*$$$ quantification in the liver using a stack-of-stars multi-echo acquisition with respiratory-resolved model-based reconstruction. Magn Reson Med 2020;84:2592-2605.
- Tan Z, Voit D, Kollmeier JM, Uecker M, Frahm J. Dynamic water/fat separation and $$$B_0$$$ inhomogeneity mapping - Joint estimation using undersampled triple-echo multi-spoke radial FLASH. Magn Reson Med 2019;82:1000-1011.
- Rosenzweig S, Scholand N, Holme HCM, Uecker M. Cardiac and respiratory self-gating in radial MRI using an adapted singular spectrum analysis (SSA-FARY). IEEE Trans Med Imaging 2020;39:3029-3041.
- Uecker M, et al. BART Toolbox for Computational Magnetic Resonance Imaging. DOI: 10.5281/zenodo.592960.
- Hamilton G, Yokoo T, Bydder M, Cruite I, Schroeder M, Sirlin CB, et al. In vivo characterization of the liver fat 1H MR spectrum. NMR Biomed 2011;24:784-790.
- Uecker M, Hohage T, Block KT, Frahm J. Image reconstruction by regularized nonlinear inversion - Joint estimation of coil sensitivities and image content. Magn Reson Med 2008;60:674-682.
- Boyd S, Parikh N, Chu E, Peleato B, Eckstein J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine Learning 2010;3:1-122.
- Feng L, Grimm R, Block KT, Chandarana H, Kim S, Xu J, et al. Golden-angle radial sparse parallel MRI: Combination of compressed sensing, parallel imagin, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI. Magn Reson Med 2014;72:707-717.
- Block KT, Chandarana H, Milla S, Bruno M, Mulholland T, Fatterpekar G, et al. Towards routine clinical use of radial stack-of-stars 3D gradient-echo sequences for reducing motion sensitivity. J Korean Soc Magn Reson Med 2014;18:87-106.
Figures
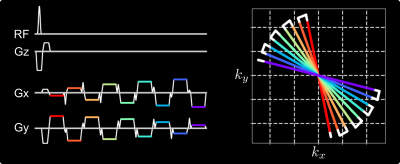
Figure 1. (Left) One representative TR block of the proposed multi-echo radial FLASH sequence. (Right) The corresponding $$$k$$$-space trajectory. In this example, 9 echoes with different k-space spokes are acquired per RF excitation. The echoes are color coded, indicating the period when the ADC is switched on, while the white solid lines indicate either the ramp or the blip gradients.
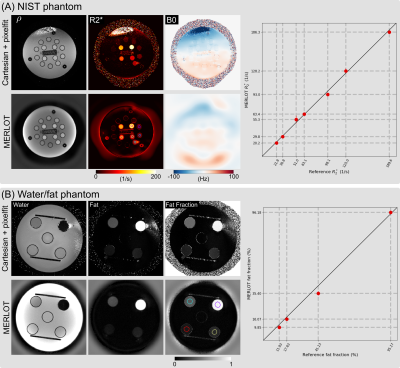
Figure 2. Comparison of (A) NIST phantom $$$R_2^\star$$$ maps and (B) water/fat phantom fat fraction maps from pixel-wise fitting of Cartesian multi-gradient-echo images (Cartesian + pixelfit) and multi-echo radial FLASH with model-based reconstruction (MERLOT), respectively. The right panel displays the correlation plot between the reference and the MERLOT values based on the depicted region of interests (ROI).
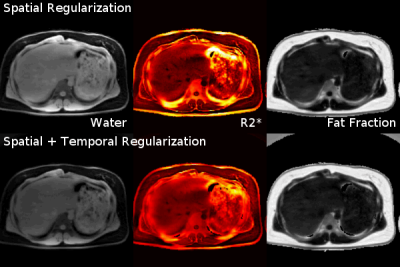
Figure 3. Comparison between regularization methods for 2D single-slice real-time acquisition. (Top) Model-based reconstruction with only spatial sparsity regularization (joint $$$\ell1$$$-Wavelet). (Bottom) Model-based reconstruction with both spatial sparsity and temporal TV regularization, which is advantageous in reducing noise and streaking artifacts.
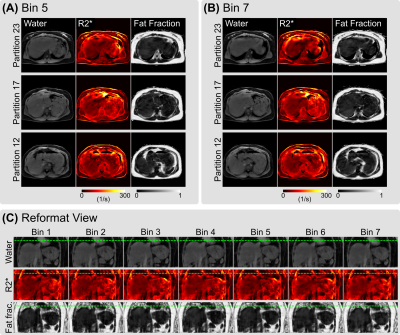
Figure 4. Model-based reconstruction of free-breathing 3D stack-of-stars multi-echo radial acquisition. SSA-FARY was employed to extract seven respiratory phases. (A) and (B) display the reconstructed water, $$$R_2^\star$$$ and fat fraction maps from three selected partitions at the 5th bin (end exhalation) and the 7th bin (end inhalation), respectively. (C) Reformatted view of all respiration phases with dotted green lines indicating the respiratory motion.
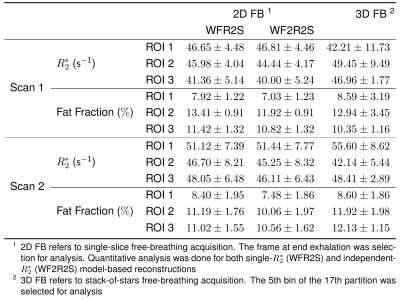
Table 1. Quantitative analysis of liver $$$R_2^\star$$$ and fat fraction from different acquisition protocols: 2D single-slice real-time acquisition (Figure 3) and 3D stack-of-stars acquisition (Figure 4).