0280
Joint estimation of coil sensitivities and image content using a deep image prior1Institute for Diagnostic and Interventional Radiology, University Medical Center Göttingen, Germany, Göttingen, Germany, 2Campus Institute Data Science (CIDAS), University of Göttingen, Germany, Göttingen, Germany
Synopsis
Parallel imaging for reduction of scanning time is now routinely used in clinical practice. The spatial information from the coils’ profiles are exploited for encoding. The nonlinear inversion reconstruction is a calibrationless parallel imaging technique, which jointly estimate coil sensitivities and image content. In this work, we demonstrate how to combine such a calibrationless parallel imaging technique with an advanced neural network based image prior for efficient MR imaging.
Introduction
Model-based reconstruction with regularization terms on the image is flexible and efficient in improving the reconstruction quality when k-space data is highly undersampled. Recently, several deep learning based reconstruction methods have been proposed for MRI acceleration. However, most of them rely on specific sampling patterns and precomputed coil sensitivities for supervised training, limiting their flexibility in applications. In this work, we present an approach to jointly estimate the coil sensitivities and image regularized by an image prior [2] that is sampling pattern independent. Furthermore, we validated the proposed method with radial k-space data acquired for a human brain.Theory
Parallel MR imaging can be formulated as a nonlinear inverse problem as follow$$F(\rho, c):=(\mathcal{F}_S(\rho\cdot c_1), \cdots, \mathcal{F}_S(\rho\cdot c_N)) = {y},$$
where $$$\mathcal{F}_S$$$ is an undersampled Fourier transform operator and the corresponding k-space data is $$${y} = (y_1, \cdots, y_N)^T$$$, $$$\rho$$$ denotes the spin density and $$${c}=(c_1, \cdots, c_N)^T$$$ denotes coil sensitivities. Proposed in the nonlinear inverse reconstruction (nlinv) [1], this problem can be solved with the Iteratively Regularized Gauss Newton Method (IRGNM) by estimating $$$\delta m:=(\delta \rho, \delta c)$$$ in each step $$$k$$$ for given $$$m^k:=(\rho^k, c^k)$$$ with the following minimization problem
$$\underset{\delta x}{\min} \frac{1}{2}\|F'(m^k)\delta m+F(m^k) - \boldsymbol{y}\|_2^2 + \frac{\alpha_k}{2}\mathcal{W}(\boldsymbol{c}+\delta c) + \beta_k{R}(\rho^k+\delta \rho),\quad (1)$$
where $$$\mathcal{W}({c})=\|W{c}\|^2=\|w\cdot\mathcal{F}{c}\|$$$ is a penalty on the high Fourier coefficients of the coil sensitivities and $$$R(\rho)$$$ is a regularization term on $$$\rho$$$. The $$$\alpha_k$$$ and $$$\beta_k$$$ decay based on reduction factor over iteration steps. In this work, the neural network based log-likelihood prior was investigated [2], formulated with following joint distribution
$$\log P(\hat{\Theta}, \boldsymbol{x}) = \log p(\boldsymbol{x};\mathrm{NET}(\hat{\Theta}, \boldsymbol{x}))=\log p(x^{(1)})\prod_{i=2}^{n^2} p(x^{(i)}\mid x^{(1)},..,x^{(i-1)}),$$
where the neural network $$$\mathrm{NET}(\hat{\Theta}, \boldsymbol{x})$$$ outputs the distribution parameters of the mixture of logistic distribution which was used to model images. For each step, the fast iterative gradient descent method (FISTA) [3] is used to minimize Eq (1). The proximal operation on $$$\log P(\hat{\Theta}, \boldsymbol{x})$$$ was approximated using gradient updates. The gradient of $$$\log P(\hat{\Theta}, \boldsymbol{x})$$$ is computed via backpropagation.
Methods
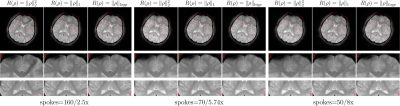
To obtain a generic image prior for the nonlinear inversion reconstruction, we trained the PixelCNN++ with aliased-free brain images. Then, the computation graph of the neural network and the trained model were exported with TensorFlow. The inference using the trained model was implemented via TensorFlow C API within BART toolbox's framework. The optimization algorithm was then based on existing functionality in BART.For validation, T2$$$^*$$$-weighted data (TE=16ms, TR=770ms, 3T) from a human brain was acquired with a GRE sequence. The image matrix was 256$$$\times$$$256 and the resolution was 1mm$$$\times$$$1mm. We acquired 160 radial k-space spokes using golden angle radial trajectory (2.5-fold acceleration). The gradient delay of radial trajectories was estimated with RING [4]. The number of channels was compressed to eight. At last, we reconstructed images from a different number of spokes (50, 70, 160) and made comparisons of different regularization terms that includes $$$\ell_2$$$, $$$\ell_1$$$-wavelet and learned log-likelihood.
Results
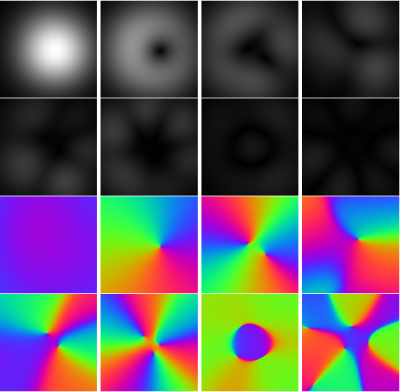
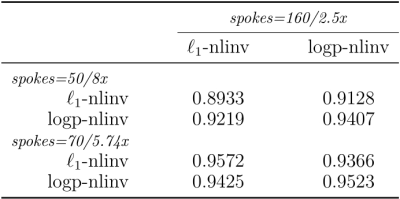
The comparisons of reconstructions using different regularization were shown in Figure 1, including the moderate undersampling (2.5-fold acceleration) and the high undersampling k-space data (5.74-fold/ 8-fold acceleration). The learned log-likelihood prior tends to smooth images and suppress noises but preserves the boundaries between tissues well. One set of coil sensitivities estimated from 50 radial k-space spokes is shown in Figure 2. Figure 3 presents the structural similarity indices of reconstructions from different numbers of radial k-space spokes.Conclusion and Discussion
We demonstrated how a learned log-likelihood prior trained from aliased-free images can be incorporated into calibration-less parallel imaging compressed sensing reconstruction using nonlinear inversion. One advantage of the proposed method is that the same prior can be used with different sampling patterns. Learning the intrinsic relationship between the pixels from aliased-free images, the log-likelihood prior shows better performance over $$$\ell_1$$$-wavelet prior.Acknowledgements
Supported by the DZHK (German Centre for Cardiovascular Research). We gratefully acknowledge funding by the "Niedersächsisches Vorab" initiative of the Volkswagen Foundation and funding by NIH under grant U24EB029240. We acknowledge the support of the NVIDIA Corporation with the donation of one NVIDIA TITAN Xp GPU for this research. At last, the sincere gratitude to colleagues for insightful discussions and suggestions.References
[1] Uecker M et al., "Image reconstruction by regularized nonlinear inversion—joint estimation of coil sensitivities and image content." Magnetic Resonance in Medicine 60.3 (2008): 674-682.
[2] Luo G et al., "MRI reconstruction using deep Bayesian estimation." Magnetic Resonance in Medicine 84.4 (2020): 2246-2261.
[3] Beck A et al., "A fast iterative shrinkage-thresholding algorithm for linear inverse problems." SIAM journal on imaging sciences 2.1 (2009): 183-202.
[4] Rosenzweig S, Holme HCM, Uecker M. "Simple auto‐calibrated gradient delay estimation from few spokes using Radial Intersections (RING)." Magnetic resonance in medicine 81.3 (2019): 1898-1906.
[5] Lustig M et al. "Compressed sensing MRI." IEEE signal processing magazine 25.2 (2008): 72-82.
[6] Uecker M et al., BART Toolbox for Computational Magnetic Resonance Imaging, DOI:10.5281/zenodo.592960
Figures