0224
Robust Multi-shot EPI with Untrained Artificial Neural Networks: Unsupervised Scan-specific Deep Learning for Blip Up-Down Acquisition (BUDA)1Athinoula A. Martinos Center for Biomedical Imaging, Boston, MA, United States, 2Radiology, Harvard Medical School, Boston, MA, United States, 3Electrical Engineering, University of Southern California, Los Angeles, CA, United States, 4State Key Laboratory of Modern Optical Instrumentation, College of Optical Science and Engineering, Zhejiang University, Hangzhou, China, 5Boston Children's Hospital, Boston, MA, United States
Synopsis
Blip Up-Down Acquisition (BUDA) has been successful in generating distortion-free multi-shot EPI (msEPI) without navigators, utilizing a fieldmap and structured low-rank constraints. Recently, a scan-specific artificial neural network (ANN) motivated by structured low-rank modeling, named LORAKI, has been proposed for refined MRI reconstruction, where its training employed fully-sampled autocalibrated signal (ACS). Although applying LORAKI framework to BUDA is beneficial, acquiring fully-sampled ACS for msEPI is not practical. We propose scan-specific unsupervised ANNs for improved BUDA msEPI without training data. Experiment results indicate that the proposed BUDA-LORAKI exhibits advantages, with up to 1.5x reduction in NRMSE compared to standard BUDA reconstruction.
Introduction
Multi-shot EPI has been extensively employed for fast imaging with reduced distortion and blurring over single-shot acquisition. However, resolving shot-to-shot phase variations remains as a challenge. Blip Up-Down Acquisition (BUDA)1,2 and related approaches3,4,5 have been proposed,utilizing interleaved blip-up and -down k-space data acquisition, a fieldmap in the forward model for distortion correction and the reconstruction using structured low-rank modeling6.A recent work7 has shown that model-based structured low-rank matrix modeling8-15 can be generalized into artificial neural network (ANN) models. Its iterative structure enables the use of a small parametric space that can be trained by an autocalibration signal (ACS). It prevents potential “hallucinations” introduced from external training data which may not generalize to test acquisitions, and are advantageous when large-scale training data are unavailable. Therefore, incorporating LORAKI to BUDA will be impactful, but acquiring ACS with msEPI would necessitate uneven echo spacings, longer readouts, increased blurring, and later TEs.
In this work, we propose BUDA-LORAKI, a scan-specific unsupervised ANN for BUDA msEPI . Recent studies16, 17 have shown that the structure of ANNs can be powerful for inverse problems without training data (“untrained” neural networks18, 19).
Theory
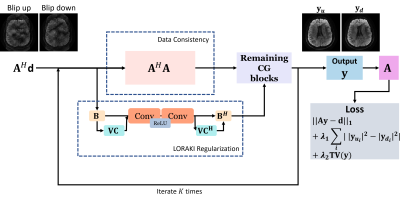
The following11 can be formulated for BUDA reconstruction using LORAKS low-rank framework8-12,$$ \min_{\mathbf{\rho}}f(\mathbf{\rho}) = \min_{\mathbf{\rho}} \| \mathbf{A}\mathbf{\rho} - \mathbf{d}\|_2^2 + \mu\mathcal{J}( \mathbf{B}\rho),$$with the BUDA forward model $$$\mathbf{A}$$$ (coil sensitivity, fieldmap, Fourier transform, and undersampling), the distortion-free images $$$\mathbf{\rho}$$$, the acquired data $$$\mathbf{d}$$$, the SENSE forward model $$$\mathbf{B}$$$ (coil sensitivity and Fourier transform), and the LORAKS regularization $$$ \mathcal{J}(\cdot)$$$. We will name this as BUDA-LORAKS.It has been shown that the low-rank methods8-15 are composed of convolutional operations, so their iterative counterparts (e.g. Landweber iteration, Conjugate Gradient) can be represented as convolutional neural network models7. Specifically, the gradient of the above objective function is $$ \nabla f(\mathbf{\rho}) = \mathbf{A}^H \mathbf{A}(\mathbf{\rho}) - \mathbf{A}^H\mathbf{d} + \mu \mathbf{B}^H (c_{\theta_2}(c_{\theta_1}(\mathbf{B}\mathbf{\rho}))),$$with $$$c_{\theta_1}, c_{\theta_2} $$$ are convolution operations corresponding to the LORAKS regularization. The LORAKI framework was introduced from this observation, by adding nonlinear ReLU activation function. Let $$$g(\mathbf{\rho})$$$ be a blind objective function for LORAKI, we define its gradient as,$$ \nabla g(\mathbf{\rho}) = \mathbf{A}^H \mathbf{A}(\mathbf{\rho}) - \mathbf{A}^H\mathbf{d} + \mu \mathbf{B}^H (c_{\theta_2}(ReLU(c_{\theta_1} (\mathbf{B}\mathbf{\rho})))),$$providing improved reconstruction by added nonlinearities7.
The proposed network structure adopted conjugate gradient (CG) algorithm20. Unlike standard LORAKI requring ACS for training, we propose to circumvent the disadvantages of incorporating ACS into msEPI by unsupervised reconstruction. We trained the network without training data, using the following loss function, let $$$\mathbf{y}= h_\theta(\mathbf{x})$$$ be the output of the proposed LORAKI network (reconstructed blip-up and -down images) with the network parameter $$$\theta$$$, $$\min_{\theta} \| \mathbf{A}(\mathbf{y}) – \mathbf{d} \|_1 + \lambda_1 \sum_i | |\mathbf{y}_{\mathbf{d}i}|^2 - |\mathbf{y}_{\mathbf{u}i}|^2 | + \lambda_2 TV(\mathbf{y}), $$with $$$ |\mathbf{y}_{\mathbf{u}i}|, |\mathbf{y}_{\mathbf{d}i}|$$$ are magnitude of reconstructed blip-up and -down images at voxel $$$i$$$, respectively. The first term enables training without the fully-sampled training data21, and second and third terms are specific to improve msEPI reconstruction, where the magnitude of blip-up and -down images should be consistent (taking magnitude prevents us from vulnerability to shot-to-shot phase variations), and the reconstructed images are spatially smooth through total variation.
Method
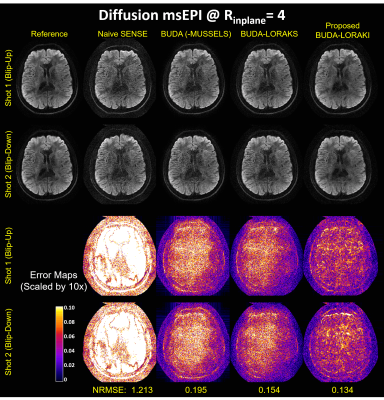
Three different dataset were acquired on 3T Siemens scanners using 32-channel reception.i. msEPI diffusion: Using a Prisma system, 1x1x4 mm3, b=1000s/mm2 diffusion data were acquired at $$$R_{inplane}$$$=4 acceleration using 4-shots (2 blip-up, 2 -down) and TE/TR=83ms/3900ms. Using all 4-shots provided a reference BUDA reconstruction, after which only 2-shots were utilized to compare undersampled reconstructions.
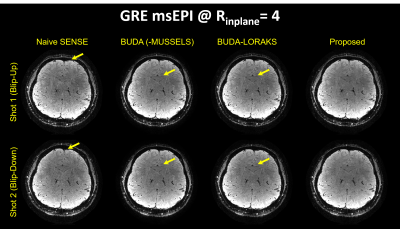
ii. 3D-EPI gradient echo: Using a Trio scanner, 1 mm3 isotropic 3D-EPI data were acquired at $$$R_{inplane}$$$=4 using 2-shots (1 blip-up, 1-down) with TE/TR=36/72ms.
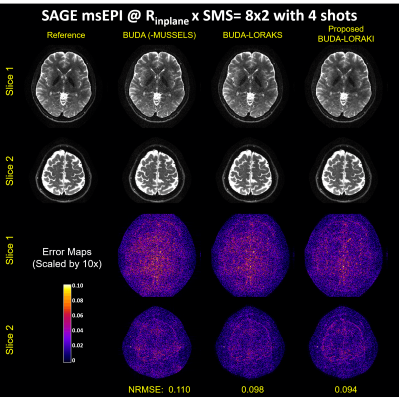
iii. msEPI SAGE: Spin-and-gradient echo (SAGE) EPI data with simultaneous multislice (SMS) encoding at $$$R_{inplane}$$$xSMS=8x2 acceleration using 8-shots (4 blip-up, 4-down) were acquired to provide reference data, and 4-shots (2 blip-up, 2-down) were used. Each SAGE acquisition provided a gradient-, a mixed-, and a spin-echo contrast. Three separate acquisitions were made to provide a total of 9 different contrasts to enable T2 and T2* mapping. TE=[18 64 91], [30 88 115], [42 112 139] ms for each contrast, TR = 5000 ms for all.
BUDA-LORAKI reconstruction results are compared with naive-SENSE, standard-BUDA (with virtual conjugate coils and MUSSELS6 low-rank constraint), and BUDA-LORAKS.
Results
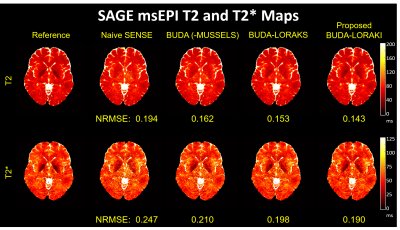
Figure 2 presents the diffusion results. The NRMSE values and the error maps indicate that the proposed BUDA-LORAKI can provide ~1.5x-reduction in error compared to standard BUDA. Figure 3 displays the results with GRE data, where the proposed method successfully corrects the distortion with mitigated aliasing artifacts. Figure 4 exhibits the SMS reconstruction results from the SAGE data, where the proposed method better mitigates noise amplification and yields the lowest NRMSE. Figure 5 shows T2 and T2* map estimation from the reconstructed 9 echoes of the SAGE SMS data. The proposed method enables improved parameter mapping with lowest NRMSE.Discussion and Conclusion
This work introduced unsupervised, untrained, scan-specific ANN for robust BUDA msEPI reconstruction without training data. While this work focused on the uniform undersampling, it can also address variations in other data acquisition settings such as various sampling patterns (e. g. random, variable sampling, and partial Fourier). Furthermore, while it only showed BUDA msEPI reconstruction, similar frameworks can easily be adapted to other types of MRI reconstruction.Acknowledgements
This work was supported by research grants NIH R01 EB028797, U01 EB025162, P41 EB030006, U01 EB026996 and the NVidia Corporation for computing support.References
1. Liao C, Cao X, Cho J, Zhang Z, Setsompop K, Bilgic B. Highly efficient MRI through multi-shot echo planar imaging. Wavelets and Sparsity XVIII, Proceedings of SPIE 11138. 2019. p. 1113818
2. Cao X, Liao C, Zhang Z, Iyer SS, Wang K, He H, Liu H, Setsompop K, Zhong J, Bilgic B. T2-BUDA-gSlider: rapid high isotropic resolution T2 mapping with blip-up/down acquisition, generalized SLIce Dithered Enhanced Resolution and subspace reconstruction; arXiv preprint. 2019. arXiv:1909.12999
3. Jezzard P, Balaban RS. Correction for geometric distortion in echo planar images from B0 field variations. Magnetic Resonance in Medicine. 1995. pp. 65–73.
4. Bhushan C, Joshi AA, Leahy RM, Haldar JP. Improved B0-distortion correction in diffusion MRI using Interlaced q-space sampling and constrained reconstruction. Magnetic Resonance in Medicine. 2014. pp. 1218–1232
5. Zahneisen B, Aksoy M, Maclaren J, Wuerslin C, Bammer R. Extended hybrid-space SENSE for EPI: Off-resonance and eddy current corrected joint interleaved blip-up/down reconstruction. NeuroImage. 2017. pp. 97–108
6. Mani M, Jacob M, Kelley D, Magnotta V. Multi-shot sensitivityencoded diffusion data recovery using structured low-rank matrix completion (MUSSELS). Magnetic Resonance in Medicine. 2017. pp. 494–507
7. Kim TH, Garg P, Haldar JP. LORAKI: Autocalibrated recurrent neural networks for autoregressive MRI reconstruction in k-Space. arXiv preprint. 2019. arXiv:1904.09390
8. Haldar JP. Low-rank modeling of local k-space neighborhoods (LORAKS) for constrained MRI. IEEE Transactions on Medical Imaging. 2014. pp. 668–681
9. Haldar JP. Autocalibrated loraks for fast constrained MRI reconstruction. IEEE International Symposium on Biomedical Imaging (ISBI). 2015. pp. 910–913.
10. Haldar JP, Zhuo J. P-LORAKS: low-rank modeling of local k-space neighborhoods with parallel imaging data. Magnetic Resonance in Medicine. 2016. pp. 1499–1514.
11. Kim TH, Setsompop K, Haldar JP. LORAKS makes better SENSE: Phase-constrained partial fourier SENSE reconstruction without phase calibration. Magnetic Resonance in Medicine. 2017. pp. 1021–1035.
12. Haldar JP, Setsompop K. Linear Predictability in Magnetic Resonance Imaging Reconstruction: Leveraging Shift-Invariant Fourier Structure for Faster and Better Imaging. IEEE Signal Processing Magazine. 2020. PP. 69-82.
13. Shin PJ, Larson PEZ, Ohliger PA, Elad M, Pauly JM, Vigneron DB, Lustig M. Calibrationlessparallel imaging reconstruction based on structured low-rank matrix completion. Magnetic Resonance in Medicine. 2014. pp. 959–970
14. Jin KH, Lee D, Ye JC. A general framework for compressed sensing and parallel MRI using annihilating filter based low-rank hankel matrix. IEEE Transactions on Computational Imaging. 2016. pp. 480–495.
15. Ongie G, Jacob M. Off-the-grid recovery of piecewise constant images from few Fourier samples SIAM Journal on Imaging Sciences. 2016. pp. 1004–1041.
16. Ulyanov D, Vedaldi A, Lempitsky V. Deep image prior. IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 2018. pp. 9446–9454.
17. Heckel R, Hand P. Deep Decoder: Concise image representations from untrained non-convolutional networks. International Conference on Learning Representations (ICLR). 2019.
18. Arora S, Roeloffs V, Lustig M. Untrained Modified Deep Decoder for Joint Denoising and Parallel Imaging Reconstruction. International Society for Magnetic Resonance in Medicine Virtual Conference & Exhibition. 2020. p. 3585
19. Darestani MZ. Heckel R. Accelerated MRI with Un-trained Neural Networks. arXiv preprint. 2020. arXiv:2007.02471
20. Aggarwal HK, Mani MP, and Jacob M. MoDL: model based deep learning architecture for inverse problems. IEEE Transactions on Medical Imaging. 2018. pp 394–405
21. Tamir JI, Yu SX, Lustig M. Unsupervised Deep Basis Pursuit: Learning inverse problems without ground-truth data. arXiv preprint. 2019. arXiv:1910.13110
Figures